Como dividimos

En la unidad anterior nos centramos en conceptos como ¿qué es la división? y ¿para qué nos sirve?, previamente también conocimos la relación que existe entre la división y la multiplicación. Es momento de que nos concentremos en el procedimiento que se utiliza para dividir dos números, pero primero consideremos las partes de la división.
Partes de la división:
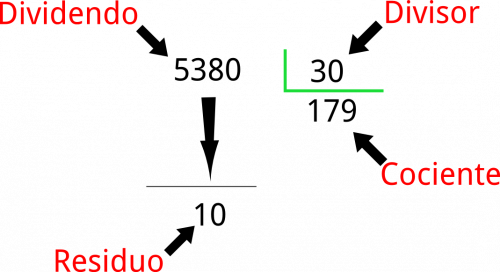
Los nombres de las partes de la división se han de aprender en los primeros años de nuestros cursos de matemáticas, pero es debido que repasemos un poco de ellas.
Dividendo: es la cantidad que queremos distribuir en partes iguales.
Ej: si nos pagan $100.000 por pintar la casa los repartiremos por mitades o en otras palabras 100,000 / 2
Divisor: es el número por el cual dividiremos la cantidad indicada, también puede verse cómo el número de partes en que se distribuirá cierta cantidad.
Ej: repartiremos los 21 mangos entre 3 personas o en otras palabras 21 / 3
Cociente: es el resultado de la división.
Residuo: es el número que sobra de la división, es decir, la parte que no se ha podido distribuir porque la división no es exacta.
La división:
En matemáticas, para dividir solo basta seguir una serie de pasos, para los cuales se requiere conocer las partes de la división y evitar confusiones al momento de operar. Este proceso estándar nos permite encontrar cocientes entre números grandes.
Ahora dividamos 3560 entre 20, consideremos escribirlo de la siguiente manera:

Como ya reconocemos el sistema decimal sabemos que el número 3560 cuenta con 3 unidades de mil, 5 centenas, 6 decenas y 0 unidades, luego, tomemos las unidades de mil y decimos cuantas veces esta el 20 en el 3, como el 20 no cabe ni una sola vez en el 3 tomamos las centenas osea el 5 y así tendremos 35.

y repetimos el procedimiento,<< cuantas veces está el 20 en el 35 >> y buscamos un número que multiplicado por 20 de igual o cercano a 35, si multiplicamos 20 x 2 sería igual a 40 y no cumpliría con la regla, pero si multiplicamos 20 x 1 se ajustaría perfectamente con la regla, así que ponemos 1 en el cociente y lo multiplicamos por 20 y el resultado lo pondremos debajo del dividendo, exactamente bajo el 35 de tal forma que sea posible hacer una resta.
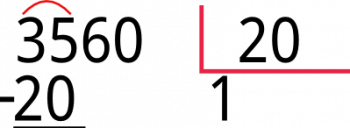
Luego restamos 35 – 20

como podemos apreciar el resultado es 15, lo siguiente que haremos será bajar el siguiente dígito y ubicarlo al lado de éste nuevo número, para nuestro caso concreto es el 6 y el número que resulta es el 156.
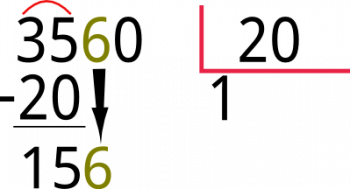
Volvemos a hacer el mismo procedimiento, un número que multiplicado por 20 nos de 156 o cercano, osea el 7 pues 20 x 7 =140 el 7 se ubica en el cociente y 140 debajo del 156 y se restan.
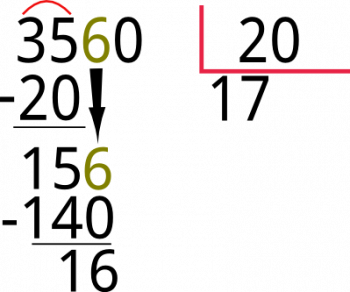
Seguido bajamos el 0 al lado del 16 y el resultado es 160.
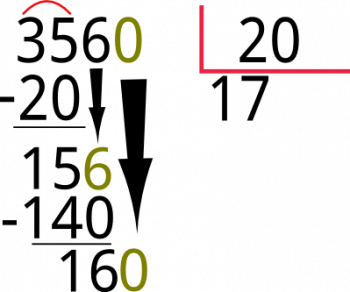
ahora buscamos un número que multiplicado por 20 de 160, el resultado es 8 ya que; 20 x 8 = 160, ubicamos el 160 bajo el 160 del dividendo y restamos.
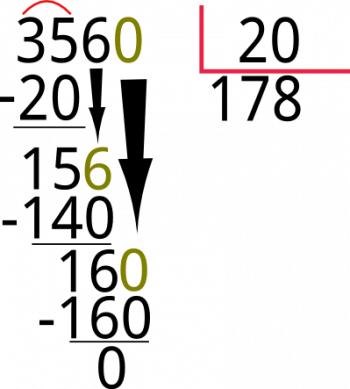
Imagine que tiene 3560 libros para repartir a 20 compañeros, según la división anterior a cada persona le tocaría 178 libros.
Ahora dividamos 3560 entre 22.

como vemos en el residuo nos queda 18 y en el cociente 161, ¿acaso quedó mal hecha la división?,¿podemos seguir dividiendo?
No, la división esta bien, solo nos indica que la forma más equitativa de repartir los libros a cada persona es de 161 libros y quedan 18 que no se pudieron repartir, pues no es justo que ha ciertas personas les toquen mas que a otras. En cuanto a si se puede seguir dividiendo ese será nuestro siguiente punto, por ahora resolvamos los siguientes ejercicios de práctica:
Resuelva las siguientes divisiones y señale las respuestas correctas encerrándolas en un círculo.
Resuelva las siguientes divisiones inexactas, indique la respuesta y el residuo con una R, por ejemplo 175 ÷ 3 = 58 , R 1.
| R = | ||
| R = | ||
| R = | ||
| R = |
Retomemos la pregunta anterior ¿podemos seguir dividiendo cuando el residuo sea menor al divisor?, la respuesta es si para ello solo debemos añadir un 0 al residuo y una coma en el cociente y continuar nuestra división, dividamos 253 ÷ 6

Como puedes apreciar en la imagen anterior diríamos que la respuesta es 6 y el residuo 1, pero como ya dijimos antes podemos seguir dividiendo, primero agregamos un 0 al residuo.

ahora que el residuo es mayor que el divisor agregamos una coma al cociente.

Continuamos operando, un número que multiplicado por 6 cercano a 10, tenemos que 6 x 1 = 6, ahora restamos 10 – 6 = 4, como 4 sigue siendo menor que el divisor agregamos un 0 al 4 para que nos quede 40 y continuamos operando, un número que multiplicado por 6 cercano a 40, multiplicamos 6 x 6 = 36 y restamos 40 – 36 = 4, ¿ qué pasó?, ¿qué pasa si volvemos al mismo número?, pues bueno si repetimos el procedimiento volveremos a llegar a 4 una cantidad infinita de veces y en el cociente pasará lo mismo, el 6 se repetirá infinitas veces.
Debemos tener muy presente que después de colocar la primera coma en el cociente, ya no es necesario poner más, esto quiere decir que la primera coma de decimal es también la única.
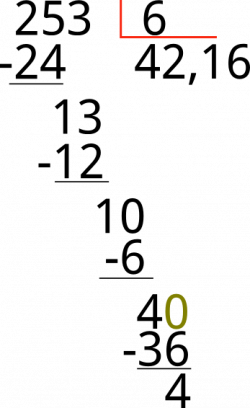
El resultado entonces será 41,16. La idea es dividir el residuo hasta llegar a 0, pero como vemos no siempre es posible que se cumpla esto.
Realice las siguientes divisiones y señale las que tengan la respuesta correcta.
22 ÷ 4 = 5.5
223 ÷ 5 = 44,6
115 ÷ 4 = 30,75
419 ÷ 8 = 52.375
En ocasiones puede que dividamos dos números y la respuesta no resulte en un número con decimales exactos, en otras palabras cuando pareciese que la división siguiera eternamente, bueno pues Lo que debemos hacer es aproximar el resultado a un número deseado de cifras decimales. Esto nos permite llegar a una respuesta que, sin ser 100 % exacta, si nos permite acercarnos considerablemente a la realidad. Para entender mejor esta idea, dividamos 96 por 7, escriba el cociente hasta llegar a cuatro cifras decimales, y después aproxime su respuesta a dos cifras decimales. Al realizar la división hasta cuatro cifras decimales, su resultado será:
donde los tres puntos seguidos indican el resultado no es exacto y continua, lo que podemos hacer es redondear. Para esto hay que seguir ciertas reglas miremos:
Para redondear debemos empezar evaluando de derecha a izquierda.
1. Dígito menor que 5: Si el siguiente decimal es menor que 5, el anterior no se modifica. Ejemplo: 12,612. Redondeando a 2 decimales se debe tener en cuenta el tercer decimal: 12,612≈ 12,61.
2. Dígito mayor o igual que 5: Si el siguiente decimal es mayor o igual que 5, el anterior se incrementa en una unidad.
- Ejemplo: 12,618. Redondeando a 2 decimales se debe tener en cuenta el tercer decimal: 12,618 ≈ 12,62
- Ejemplo: 2,3571 redondeado a la centésima es 2,36 , debido a que 2,3571 está más cerca de 2,36 que de 2,35.
Así para nuestro número eliminaríamos los números 1,4 y 2 pues como dice la regla son menores a 5.
Realice las siguientes divisiones y aproxime.
60 ÷ 7 =
175 ÷ 6 =
259 ÷ 4 =
59 ÷ 7 =
¿Qué pasa cuando el divisor tiene mas de dos números?,observemos.
Dividamos 560 ÷ 75:
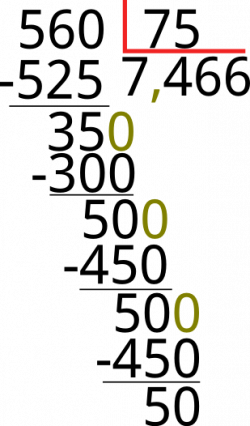
Para dividir un número cuando el divisor tiene dos dígitos se debe realizar el mismo procedimiento, en nuestro caso decimos << cuantas veces está el 75 en el 560>> así que buscamos un número que multiplicado por 75 de 560 o cercano a este, el 7, 75 x 7 = 525, restamos 560 - 525 = 35 como el 75 no cabe ni una vez en 35 agregamos un cero para que quede 350 y también una coma al cociente, repetimos el procedimiento. 75 x 4 = 300, restamos 350 – 300 = 50, agregamos un 0 al 50 para que sea divisible por 75 continuamos. 75 x 6 = 450, 500 – 450 = 50, repetimos el procedimiento anterior y volverá a dar 50 infinitas veces así que el resultado será 7,466666666... ahora redondeemos.
Redondeemos a 2 cifras decimales, empezamos de derecha a izquierda como todos son 6 podemos aproximar el siguiente 6 a 7 hasta que nos quede 7,47, podríamos aproximar a 7,5 pero como dijimos anteriormente lo dejaremos con 2 cifras decimales, por lo tanto el resultado es 7,47.
Realice las siguientes divisiones:
258 ÷ 12 =
357 ÷ 14 =
776 ÷ 16 =
712 ÷ 54 =
528 ÷ 36 =
1984 ÷ 64 =
Otro caso en la división es que uno o los dos números de la división sean decimales por ejemplo 7.5 ÷ 0.3, en este caso solo debemos multiplicar por una potencia de 10 ambos números hasta que no sean decimales en el caso anterior debemos multiplicar ambos números por 10 así:
De esta manera ya solo dividiremos 75 ÷ 3 = 25 y este será el resultado.
También es posible que el dividendo sea menor al divisor por ejemplo 2 ÷ 5, para realizar esta división solo debemos agregar un 0 al dividendo, un cero y una coma al cociente. Miremos:
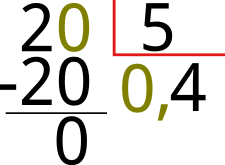
Continuamos haciendo la división normalmente, buscamos un número que multiplicado por 5 de 20 o cerca a 20, el 4, restamos
20 - 20 = 0 y la división estará completa.
Realice los siguientes ejercicios:
4 / 8 =
8 / 12 =
73 / 100 = 0.70
5 / 20 =
20 / 100 = 0.20
12 / 14 = 0.86