Introducción proporciones directas e inversas

Hoy en día vemos las proporciones en los diseños arquitectónicos, en la solución de diferentes problemas de ingeniería y en la vida cotidiana en el sector rural y entre muchos otros campos. Para entender mejor el concepto de proporciones hay que tener en cuenta el concepto de razón y ver su utilidad en la solución práctica de problemas que tiene ver con situaciones cotidianas, como por Ejemplo en las construcciones rurales…

En este capítulo encontraremos una serie de conceptos: Proporcionalidad directa e inversa, Razón, proporción y ejemplos que amplían estas definiciones; que nos ayudan a crear la destreza de interpretar, graficar y solucionar situaciones de la vida rural, y a la vez para darle cumplimiento a los estándares básicos de competencias en matemáticas.

PROPORCIONALIDAD DIRECTA

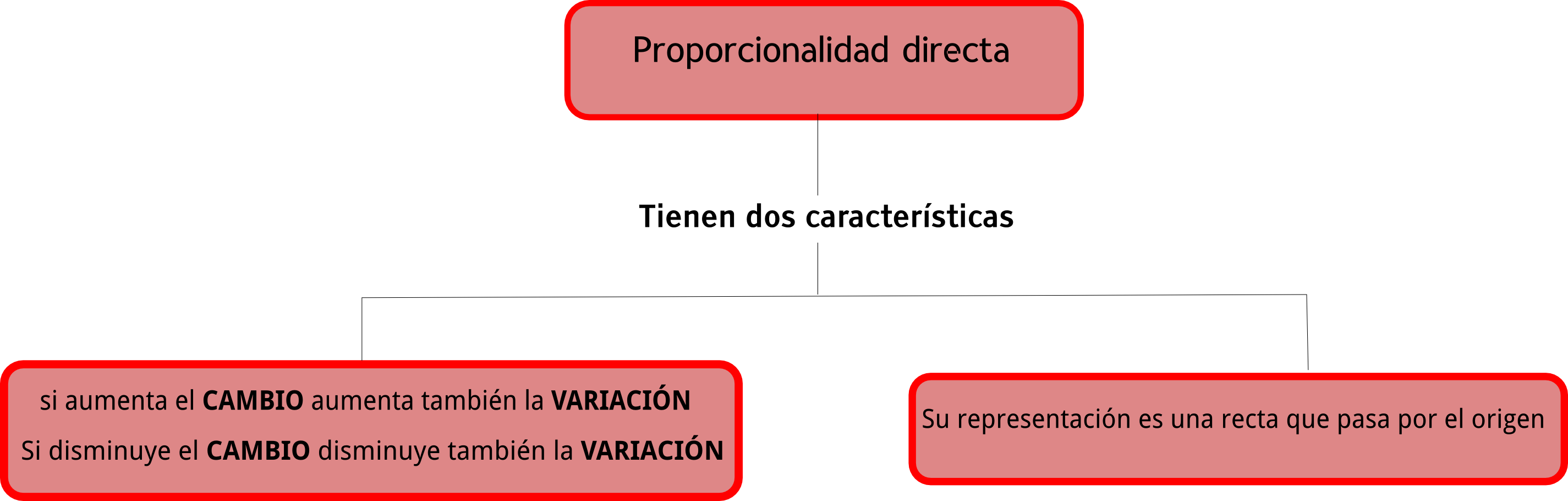
Concepto. Dos magnitudes son directamente proporcionales si al aumentar una, aumenta también la otra; si al disminuir la primera, la segunda también disminuye y, además, tiene cociente constante. En este caso se dice que existe proporcionalidad directa y la representación gráfica es una línea recta que pasar por el origen de una recta. También, Si se tiene 2 cantidades tales que al multiplicar una de ellas por un número la otra queda multiplicada por el mismo número, o al dividir una de ellas la otra queda dividida por el mismo número, se dice que las cantidades son directamente proporcionales.

Ejemplo: Si 18 lapices cuestan $28, entonces 54 lápices constarán el triple, es decir, $ 84; al multiplicar el número de lápices por 3 el costo también quedó multiplicado por 3, por lo tanto, las cantidades son directamente proporcionales.

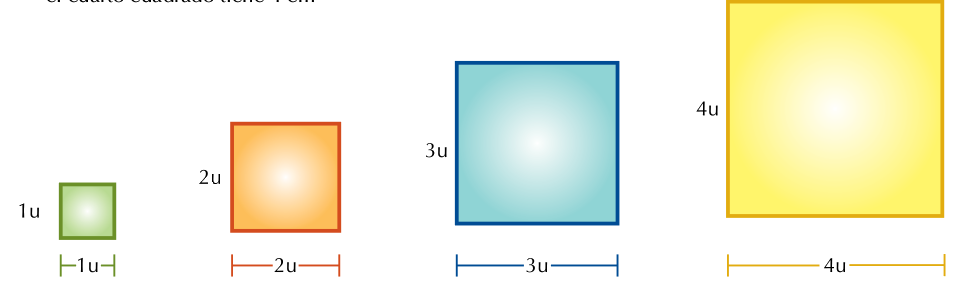
Ejemplo: La ilustración muestra una secuencia de cuadrados, que va aumentando de acuerdo al tamaño del lado. Así: EL primer cuadrado tiene 1 cm de lado, es segundo tiene 2 m, el tercero tiene 3 cm y el cuarto cuadro tiene 4 cm.

Recordemos que el perímetro de una figura es la longitud de su contorno, es decir, la suma de los todos sus lados:

Llamamos P al perímetro de los cuadros, esto es:

P1 = 1 cm + 1 cm + 1 cm + 1 cm = 4 x 1 cm = 4 cm

P2 = 2 cm + 2 cm + 2 cm + 2 cm = 4 x 2 cm = 8 cm

P3 = 3 cm + 3 cm + 3 cm + 3 cm = 4 x 3 cm =12 cm

P4 = 4 cm + 4 cm + 4 cm + 4 cm = 4 x 4 cm = 16 cm

Así Cuando el lado es 1, el perímetro es 4, entonces, se representa en la gráfica con el punto (1,4) Cuando el lado es 2, el perímetro es 8, entonces, se representa en la gráfica con el punto (2,8)

Cuando el lado es 3, el perímetro es 12, entonces, se representa en la gráfica con el punto (3,12)
Cuando el lado es 4, el perímetro es 16, entonces, se representa en la gráfica con el punto (4,16)

Si la longitud de un cuadrado aumenta, entonces el perímetro también aumenta. Es decir, si la longitud del lado del cuadrado cambia entonces, el perímetro también varía. Si la longitud del lado de un cuadrado fuera 10 unidades (u), entonces, el perímetro sería.

P10: 10u + 10u + 10u + 10u = 4 x 10u = 40u

Si la longitud del lado de un cuadrado es 20u entonces el perímetro es

P20 = 20u + 20u + 20u + 20u = 4 x 20u = 80u

Por lo tanto el valor del perímetro de un cuadrado depende de la longitud del lado.

Si determinamos la razón entre la longitud de cada longitud de los lados del cuadro y su respectivo perímetro, se obtiene cocientes constantes.:

¼ = 0.25 2/8 = 0.25 3/12 = 0.25 4/16 = 0.25

En Conclusión: Si se Cambia la longitud del lado de un cuadrado, el perímetro del mismo cuadrado cambia 4 veces el valor de longitud del lado.

Razón. Es el cociente (división) entre 2 cantidades, donde el numerador recibe el nombre de antecedente y el denominador de consecuente. Para las cantidades a, b en la razón a/b o a:b con b diferente a Cero, a recibe el nombre de antecedente y b el de consecuente.

Ejemplos.

En la razón 7/4, 7 es el antecedente y 4 es el consecuente.

En la razón 2:3 (se lee 2 es a 3), 2 es el antecedente y 3 es el consecuente.

Proporción.

Es la igualdad entre dos o más razones.

A/b = c/d o bien a:b::c:d con b diferente 0 y d diferente 0

La expresión se lee a es a b como c es a d, a y d son los extremos, b y c son los medios.

En la proporción 2/5 = 4/10 los extremos son 2 y 10; a su vez 5 y 4 son los medios.

Ejemplo.

3 es a 6 como 8 es a 16, se escribe 3/6 =8/16

Al simplificar cada fracción se obtiene ½, la razón de proporcionalidad. Es una proporción el producto de los extremos es igual al producto de los medios.

A/b = c/d o bien a:b::c:d con b diferente 0 y d diferente 0

Ejemplos

Para la proporción 5/4 = 20/16 se tiene que (5)(16) = (4)(20) = 80

En una proporción un extremo es igual al producto de los medios dividido por el extremo restante, es decir:

                      a/b = c/d entonces a = b.c/d o d = b.c/a

Ejemplo. Hallar el valor de m en la siguiente proporción m/5 = 20/30

Solución

m es un extremo en la proporción, entonces:

m: (5)(24)/30 = 120/30 = 4

Recordemos que se denomina proporción a la igualdad de dos razones y se presenta como:

a/b = c/d o a : d = b : c

A los términos a y d de la proporción se les conoce como extremos y a los términos c y b de la proporción se les conoce como medios. Si se multiplica entre sí los extremos y los medios, obsérvese lo que sucede.

2 x 10 = 20 y 4 x 5 = 20

Si a/b = c/d entonces a x d = c x b

La propiedad fundamental de las proporciones tiene su utilidad en la solución de problemas en que, dada una proporción, se desconocen algunos de sus términos.

En efecto, los productos obtenidos son iguales, por lo que: En toda proporción, el producto de los medios es igual al producto de los extremos. A esta característica se le llama propiedad fundamental de las proporciones.

Veamos un Ejemplo:

En un arreglo floral, por cada 9 margaritas, se le colocan 3 rosas; si en un arreglo hay 5 rosas, ¿Cuántas margaritas se podrán contar? Estableciendo las razones correspondientes, obtenemos la igualdad:

M/5 = 9/3

Como el número de margaritas que se podrán cortar aún no se conocen, se reemplaza por la M. El valor de M Puede obtenerse así: Como el producto de los medios es igual al producto de los extremo, entonces M x 3 = 9 x 5 De donde se obtiene que: M = 3 X 5/3 Entonces M = 15 En el arreglo se podrá contar con 15 margaritas.

Lo que se comprueba al igualar el producto de medios y extremos

15 x 3 = 9 x 45

    45  = 45

PROPORCIONALIDAD INVERSA

Sí se tienen dos cantidades tales que al multiplicar una de ellas por un número, la otra queda dividida por el mismo número y viceversa, entonces, las cantidades se dicen que son inversamente proporcionales.

Ejemplo: Sí 18 hombres cavan un estanque en 12 días, entonces 6 hombres cavarán el mismo estanque en el triple del tiempo, es decir, 36 días. Al dividir el número de hombres por 3, el número de días quedó multiplicado por 3, por consiguiente las cantidades son inversamente proporcionales.