Multiplicacion o Producto

Todos los pueblos mencionados anteriormente y muchos más usaban la multiplicación o producto como un método mucho mas eficaz de contar, para conocer la cantidad de un material cualquiera que poseían y el cual intercambiarían por otro que necesitaran y que también debían de contar para estar seguros de que el intercambio era justo. Nada de esto es extraño para nosotros ya que situaciones similares se viven en nuestras comunidades en el diario vivir.
En el párrafo anterior se dijo que la multiplicación era un método de conteo más eficaz; para comprender mejor esta idea veamos el siguiente ejemplo que nos puede llevar a una definición concreta:
Muchas familias campesinas se dedican a la cosecha de alimentos como el frijol, el maíz, el café, entre otros y en conjunto con otras familias de la misma comunidad realizan el proceso necesario para comercializar el alimento o la transformación del mismo, con el objetivo de generar un proceso colectivo autogestionado evitando así la migración de campesinos a las ciudades por asuntos económicos.
El producto esta listo para venderse cuando se empaca en bolsas de 1 Kg ( Kilogramo), entonces para saber cuantos kilos tenemos solo basta con contar el número de bolsas, imaginemos que tenemos 30 bolsas listas para la venta, de repente nos llegan otras 20 bolsas para poner también en venta. En este punto surge una pregunta.
¿Que harías tú para saber el número total de bolsas que están en venta?
El primer modo de saberlo es volviendo a contar todas las bolsas, es decir, las que teníamos anteriormente y las nuevas que llegaron.
La segunda forma es simplemente sumando las bolsas que llegan nuevas y las que estaban antes.
Así podemos verificar que la suma es una forma abreviada de contar.
Ahora, si ordenamos la producción sacando 25 bolsas diarias cuantas tendremos en una semana?
Sabemos que la semana tiene 7 días, ¿cual sería el procedimiento para conocer la producción semanal?
El primer modo sería sumar 7 veces el número 25, es decir:
25 + 25 + 25 + 25 + 25 + 25 + 25
El segundo modo es multiplicar 7 x 25
Entonces la producción semanal es 175
Sin importar el método que usemos el resultado será el mismo, pero el tiempo empleado es mayor si usamos el modo uno. Así podemos verificar que la multiplicación es una abreviación de la suma y de contar.
Por ejemplo; tenemos el siguiente arreglo: Una disposición de bolas rojas de cuatro filas con tres columnas.

Para saber cuantas bolas rojas tenemos en el arreglo podemos contarlas o simplemente multiplicar el número de filas por el número de columnas y así lo sabremos con más rapidez.
Con lo visto anteriormente llegamos a la conclusión de que la multiplicación es un método mas eficaz de contar y así podremos darle una definición:
“La multiplicación o producto es la operación Aritmética que consiste en hallar el resultado de sumar un número tantas veces como lo indique otro número.” Para entender aún mas la relación existente entre sumar y multiplicar realicemos los siguientes ejercicios:
| 3 + 3 + 3 + 3 = | 3 x 4= | 12 |
| 5 + 5 + 5 + 5 + 5 + 5 + 5 = | 5 x 7= | 35 |
| 10 + 10 +10 +10 + 10 + 10 = | ||
| 12 + 12 + 12 = | ||
| 1 + 1 + 1 + 1 + 1 + 1 + 1= | ||
| 20 + 20 + 20 + 20 + 20= |
Antes dimos una definición de la multiplicación pero no estaba en el lenguaje matemático, ahora construiremos la misma definición en el lenguaje que buscamos:
Nota: debemos tener siempre presente que la comprensión lectora, el lenguaje, los símbolos y las matemáticas a pesar de ser diferentes se encuentran estrechamente relacionadas, de no ser así ¿como sería posible escribir lo mismo en dos lenguajes diferentes?
Sabemos que en las matemáticas una letra puede representar cualquier número, así podremos describir la multiplicación:
a + a + a = tres veces a = 3 x a
a + a + a + a = cuatro veces a = 4 x a
a + a +a + a + a + a + a + a + a = nueve veces a = 9 x a
a +a + a + a + a + a + a + a + a + a + a + a + …..... + a = n veces a = n x a
n al ser una letra significa que puede ser cualquier número, pero no uno al azar sino el número de veces que se repite el otro número.
Cuando estábamos construyendo nuestra definición, en la primera parte la letra “a” se repite tres veces, en la segunda parte la letra “a” se repite cuatro veces, en la tercera la letra “a” se repite nueve veces y en la última parte la letra “a” se repite “n” veces lo que quiere decir que sin importar las veces que se repita la letra “a” la forma en que se opera es la misma.
Según los ejemplos la letra “n” adquirió los siguientes valores:
- n = 3
- n = 4
- n = 9
- n = las veces que se repite “a”
Ahora podemos decir que “n” no es cualquier número, sino las veces que se repite un determinado número.
Luego, en lenguaje matemático la multiplicación o producto es:
Otro aspecto importante en la multiplicación es la notación, esto quiere decir, la correcta forma de escribir la operación con el fin de poder identificar la operación en cualquier lugar.
Recordemos que al principio de este texto hablamos de los diferentes símbolos que cada pueblo utilizaba para relacionar las cantidades, en cada lugar eran diferentes por lo que ocasionaba ciertas dificultades a los viajeros, ya que debían aprender los símbolos de cada pueblo al que visitaban. La notación en matemáticas permite que su lenguaje sea universal, es decir que si nosotros en Colombia estudiamos las matemáticas y viajamos a otro país por muy lejano que se encuentre, dicho símbolos no habrán cambiado.
La multiplicación o producto se puede representar con el símbolo: x
Se parece a la letra “equis” o “x” pero no lo es, es el símbolo que nos da a entender la operación que vamos a efectuar o realizar.
Ejemplo:
- 4 x 3
- 23 x 2
- 11 x 5
Existen otros signos que también representan la multiplicación pero solo veremos uno de ellos, este es: .
Ejemplo:
- 4 . 3
- 23 . 2
- 11 . 5
Otra forma de notación que podremos ver mas adelante en temas como Áreas y Volúmenes es la siguiente:
Ejemplo:
| (4)(3) = | 4(3) = | (4)3 |
| (23)(2) = | 23(2) = | (23)2 |
| (11)(5) = | 11(5) = | (11)5 |
Cuando tenemos dos números entre paréntesis o cualesquiera de las formas del ejemplo anterior, la operación a realizar es una multiplicación.
Como ya vimos pues, hay diferentes formas de representar dicha operación Aritmética, pero cada forma no se utiliza por alguna razón en especial, sino por gusto del escritor, así que independientemente de la notación que veamos en cualquier texto o en el aula de clase o la que ustedes utilicen, podremos identificar que se trata de una multiplicación o producto. En otras palabras, la notación es importante en un ámbito universal, es decir para que cualquier persona de este planeta la entienda, ¿cual usar al momento de escribir? No importa siempre y cuando sean alguna de las que vimos antes.
Elemento identidad (neutro)
La identidad multiplicativa es 1; el producto de todo número multiplicado por 1 es sí mismo. Esto se conoce como la propiedad de identidad
Ejemplos:
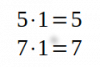
Elemento cero (absorvente)
Cualquier número multiplicado por 0 da como producto 0. Esto se conoce como la propiedad 0 de la multiplicación.
Ejemplos:
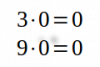
Practiquemos un poco
| (4)(3) = | 5(3) = | (4)2 = | 213 x 1 = | 1 x 0 |
| (2)(2) = | 3(2) = | 3 x 5 = | 213 x 0 = | 1 x 1 |
| 11 . 0 = | 1 x 5 = | (10)5 = | 4 . 4 = | 0 x 0 |
| 5 . 6 = | 6 x 3 = | 7 x 2 = | 14 x 1 = | 9 . 2 |
¡¡¡Intenta construir las tablas de multiplicar, es sencillo!!!
2 x 1 = 2
2 x 2 = 2 + 2 = 4
2 x 3 = 2 + 2 + 2 = 6
......
2 x 8 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 16
2 x 9 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18
2 x 10 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 +2 = 20
¡¡¡Y de forma similar con todos, absolutamente todos los números!!!
Puedes practicar más dando click en el link que aparece aquí abajito, recuerda que la práctica hace al maestro
Link para la zunchovirtual