Álgebra de Boole

La suma, la resta, la multiplicación y división hacen parte de las operaciones aritméticas, las cuales ya hemos estudiado de forma teórica y práctica, pero estás no son las únicas operaciones matemáticas existentes que se encuentran a nuestro alcance, entre ellas las operaciones booleanas o álgebra de Boole o simplemente lógica y aunque no será presentada a profundidad si veremos algunos conceptos básicos y también de donde surge esta área de las matemáticas.

El álgebra de Boole se denomina así gracias a George Boole, matemático autodidacta de origen Ingles que fue el primero en proponer el álgebra como parte de un sistema lógico, en otras palabras el álgebra de Boole fue un intento de utilizar técnicas algebraicas para tratar expresiones de la lógica, de este planteamiento surge un libro importante llamado “ Las leyes del pensamiento ”.

El trabajo de Boole fue tan importante que se aplica de forma generalizada en el ámbito de la electrónica, incluso representa la base de la informática, no únicamente por sus sistema de 1 y 0 (sistema binario) sino también por el desarrollo de circuitos digitales, los lenguajes de programación, los tipos de datos, procesadores, entre otros.

Tal vez no comprendamos aquellas cosas descritas en el párrafo anterior, pero las enunciamos para afirmar el alcance que tuvo el trabajo de Boole si tenemos en cuenta que lo desarrolló en el año 1847 y en la actualidad se sigue usando.

Pese a que esta área de las matemáticas se usa en diversos medios técnicos puede ser de utilidad también para nuestro lenguaje y pensamiento, debido a que la lógica nos permite ordenar de manera racional todas nuestras ideas.

Consideremos dos oraciones sencillas:

1. El sol sale por el oriente

2. La tierra es plana

procedamos a dar valores de Falso y Verdadero

- El sol sale por el oriente: Verdadero

- La tierra es plana: Falso

Conforme se muestra en el ejemplo anterior es posible asignarle a cada oración el valor de Falso o Verdadero, también es posible unir dos diferentes oraciones para formar las llamadas operaciones boolenas.

De nuevo consideremos dos oraciones sencillas:

1. La tierra es redonda

2. La luna tiene un ciclo de 28 días

luego, vamos a definir una operación booleana nombrada “Conjunción” esta es interpretada por la letra “ y “ y nos permite unir dos frases u oraciones.

La tierra es redonda y la luna tiene un ciclo de 28 días

o

La luna tiene un ciclo de 28 días y la tierra es redonda

La operación Conjunción tiene también un valor el que atribuirle y se hace de la siguiente forma:

• Nombremos a la oración 1. como A y a la oración 2. como B

• La conjunción es Falsa si A es falsa y B verdadera

• La conjunción es Falsa si A verdadera y B falsa

• La conjunción es Falsa si A es falsa y B es falsa

• La conjunción es Verdadera si A es verdadera y B es verdadera

Así, llegamos a la conclusión de que la conjunción solo puede tener el valor de verdad si las dos oraciones que la componen son verdaderas.

Existe otra manera de unir oraciones y es con la operación “ Disyunción “ esta es interpretada por la letra “ o “ ahora, formulemos dos oraciones mas para ejemplificar.

1. Los domingos voy al pueblo

2. Asisto a todas las plenarias

Utilizando la disyunción quedaría:

Los domingos voy al pueblo o asisto a todas plenarias

también

Asisto a todas las plenarias o los domingos voy al pueblo

Al igual que para la operación anterior, la disyunción tiene valores de verdad:

• Nombremos la oración 1. como A y a la oración 2. como B

• La disyunción es Falsa si A es falsa y B es falsa.

• La disyunción es Verdadera si A es verdadera y B es verdadera.

• La disyunción es Verdadera si A es verdadera y B es falsa.

• La disyunción es Verdadera si A es falsa y B es verdadera.

Así, se concluye que la disyunción solo puede ser Falsa si ambas oraciones que la componen son falsas, en el resto de los casos la disyunción es Verdadera, en otras palabras, solo se necesita que una de las dos expresiones sea verdadera para que la operación sea verdadera.

Otra operación booleana es la negación “ no “ que se representa con “ ¬ “ y consiste en cambiar el valor de verdad de una oración o preposición, veamos:

Los rayos siempre viajan de las nubes al suelo 

tenemos una oración a la que le asignaremos el valor de Verdadera, además la denominaremos como A.

Entonces si A es Verdadera y aplicamos la negación tendremos:

• A = Verdadera

• ¬A = Falsa

de forma literal sería:

• A = Los rayos siempre viajan de las nubes al suelo

• ¬A = Los rayos no siempre viajan de las nubes al suelo

probemos con una preposición negativa:

No pienso ir a recoger café

la anterior preposición se encuentra en forma negativa, ahora si nombramos a la oración como A y aplicamos la negación:

A = Falsa ¬A = Verdadera

de forma literal sería

• ¬A = No pienso ir a recoger café
• ¬¬A = Pienso ir a recoger café

En las operaciones booleanas la negación no es negar la oración, sino que consiste en cambiar el valor de verdad de la oración, es decir que si tenemos una expresión que es falsa al aplicar la negación, está cambia su valor a verdadera y si la preposición es verdadera al aplicar la negación la oración cambia su valor a falsa.

Iniciando esta unidad nos referimos a las aplicaciones que tiene al álgebra de Boole en nuestra cotidianidad, un ejemplo de ello es la informática, pero antes de profundizar debemos establecer una relación entre los valores de las operaciones booleanas (Falso y Verdadero) y la informática:

• En el álgebra de Boole las preposiciones que hacemos tienen un valor de verdad, estos son o Falso o Verdadero, pero ninguna oración puede tener ambos valores al mismo tiempo.

• En la informática se emplea un sistema de numeración diferente al que usamos nosotros, ese sistema se denomina binario y se compone únicamente por dos números, el 1 y el 0, es decir que las maquinas todo lo escriben con ese par de números, por ejemplo el número 7,289 en binario se escribe 10011001111001. Entonces la forma de relacionar este sistema de numeración y la lógica es asignando los siguientes valores:

• Falso = 0

• Verdadero = 1

y a su vez estas asignaciones se relacionan con la electrónica de la siguiente manera:

• Falso = 0 = Apagado = Sin corriente

• Verdadero = 1 = Encendido = Con corriente

Para ilustrar un poco lo mencionado haremos el próximo ejercicio, vamos a imaginar que tenemos un cable por el cual puede circular corriente eléctrica y además en nuestras manos sostenemos un interruptor o botón que permite o no el paso de la corriente.

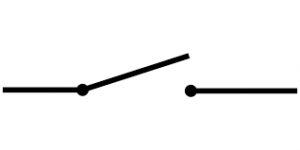
En la figura se puede ver el cable por el que circula corriente, el cual se encuentra incompleto o abierto ¿Que valor tiene este circuito?¿Que valor tendrá al completarlo o cerrarse?

Si el circuito se encuentra abierto no es posible que la corriente circule, por lo tanto el valor que le corresponde en lenguaje maquina es el 0, en el nuestro es Falso. Por el contrario, si el circuito se cierra o se completa la corriente recorre el cable y su valor en este caso sería 1 y/o Verdadero.