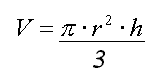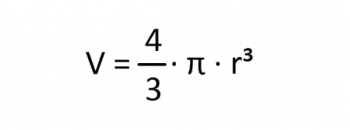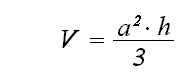Areas y volumenes
Contenido
Áreas y Volúmenes por el método de descomposición de cuerpos y figuras
Áreas
Es la superficie que existe dentro de una figura plana (2 dimensiones), también podemos decir que es la porción de tierra que se encuentra delimitada o encerrada por una cerca.
Para medir el área usamos unidades elevadas al cuadrado (m², cm², Km², entre otros).
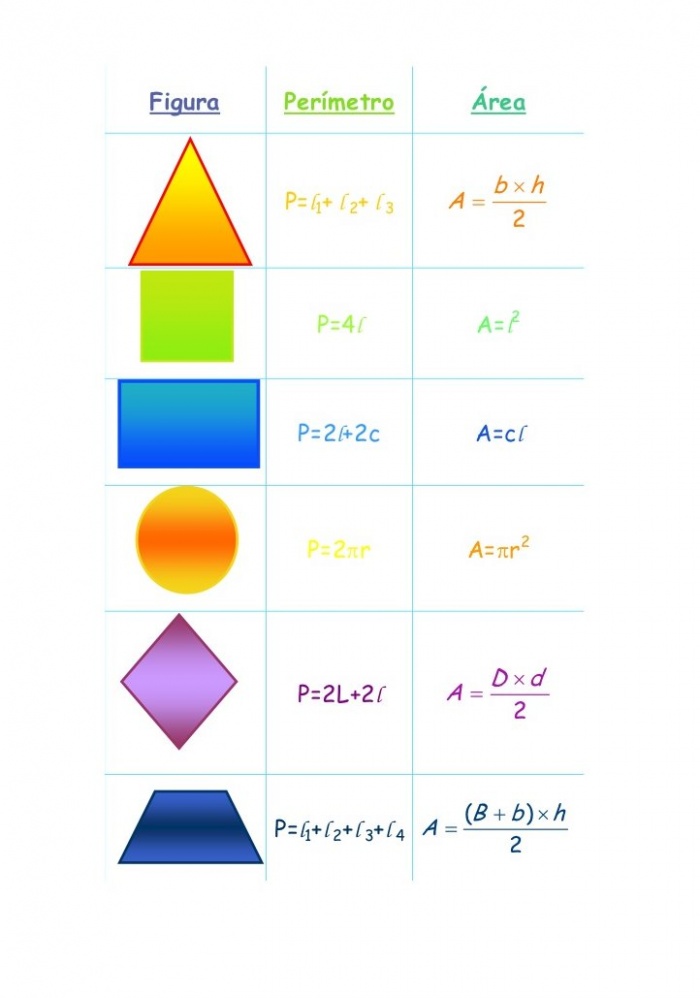
Repasemos un poco
Cuando estudiamos matemáticas aprendemos las propiedades de un mundo abstracto, de un mundo perfecto, por eso las figuras que contienen ese pedazo de tierra son triángulos, cuadrados, rectángulos, círculos, entre otros.
Ahora si queremos aplicar estas ideas del mundo abstracto al nuestro, encontraremos figuras que no tienen una formula para saber cual es su área, en ese caso podremos separar esa figura de forma extraña a unas figuras mas pequeñas que ya conocemos y con las cuales hemos trabajado con nuestro tutor o compañeros.
Digamos que tenemos un espacio para hacer piscicultura y tiene la siguiente forma:
para saber cual es el área del estanque debemos separar o descomponerlo en figuras que conozcamos, en este caso podemos ver que nuestro terreno tiene la forma de un Rectángulo y la mitad de un círculo (semi-círculo).
Como ya hemos trabajado con estas figuras antes sabemos que el área de un Rectángulo es bxh y la de un círculo es Pi(r) ² y como es medio círculo lo dividimos en 2, luego el área total es la suma de las áreas que encontramos de forma separada.
En la figura nos indican que la base del Rectángulo mide 19 y la altura 12, ahora si hacemos la separación podemos calcular las áreas por separado y luego sumarlas para hallar el área total:
Sabemos también que la altura del Rectángulo es el diámetro del semi-círculo y que el Radio es la mitad del diámetro:
Altura = Diametro ; (solo para este caso)
Radio = Diametro/2
Radio = 12/2 = 6
Área del semicirculo: Pi(r)² = Pi(6)² ; (recordemos que Pi = 3.14)
Entonces el área total es: área Rectángulo + área semi-círculo:
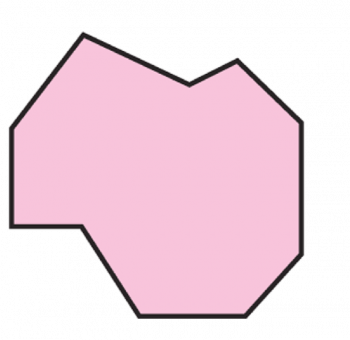
Ahora analicemos la siguiente figura:
por ejemplo, para esta figura podemos separarla en un semi-círculo, un triangulo y un rectángulo.
Ahora inténtalo con esta:
Recuerda, siempre que tengas que hallar el área de un terreno complicado debes descomponerlo en figuras comunes.
Vídeos sugeridos
https://www.youtube.com/watch?v=JfSHpD9mWCc
https://www.youtube.com/watch?v=wRdvxPOnyM4
Volúmenes
El volumen de un objeto es el espacio que ocupa, también podemos decir que es la capacidad de almacenamiento que tiene. Por ejemplo el volumen de una cubeta es la cantidad de agua que puede almacenar y para medir el volumen usamos unidades elevadas a la 3 (m³, cm³, dm³ , entre otras).
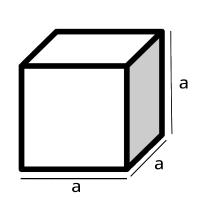
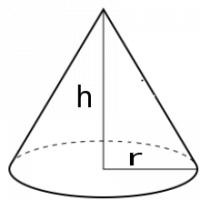
Como vimos antes hay áreas que tienen formas muy complejas para ser medidas, de manera similar hay cuerpos que debemos descomponer en otros cuerpos mas pequeños y conocidos para calcular su volumen. Hagamos un repaso de las figuras comunes:
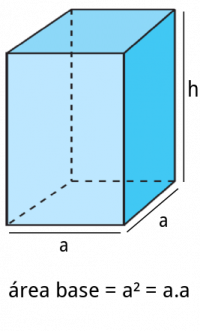
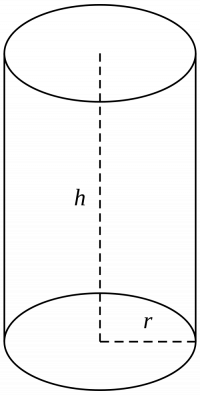
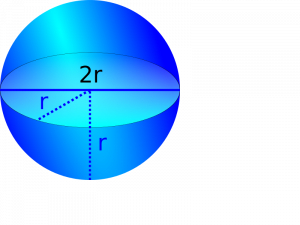
si echamos un vistazo sobre las formulas podemos ver que para todos los cuerpos (menos la esfera), se puede hallar el volumen multiplicando el área de la base y la altura del cuerpo.
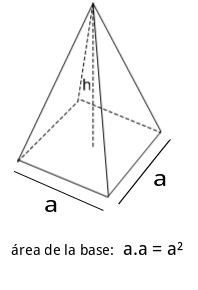
Esta información es muy útil porque el prisma es un caso especial, el prisma puede tener una base en forma de triangulo, cuadrado (como la imagen en este documento), etc.
Por eso para hallar el volumen de un prisma encontramos el área de la base y la multiplicamos por su altura.
Descomposición
Si quisiéramos calcular el volumen de un lápiz únicamente con las anteriores figuras, podríamos hacerlo?

la verdad es que no sería posible porque un lápiz como el de la imagen esta construido con un cono (en la punta), un cilindro (la parte de color amarillo) y media esfera (el borrador), así que tenemos que hallar el volumen del cono, del cilindro y la media esfera, para luego sumarla y el resultado es el volumen de todo el lápiz.
Hagamos el ejercicio juntos, toma un lápiz u objeto similar y procedamos:
vamos a separar el lápiz en tres partes, si quieres puedes usar la imaginación o partir un lápiz.
Primero separamos la punta que representa un cono, luego el cilindro y la media esfera que es el borrador.

ahora para hallar el volumen del cono (la punta) medimos su altura h y el radio r y aplicamos la formula.
Vídeo sugeridos
https://www.youtube.com/watch?v=wNVyN30MjZQ
Para el cilindro necesitamos también un radio r su altura h, pero el radio del cilindro y del cono es el mismo por lo tanto no tenemos que volver a medir el radio.
Para la media esfera solo necesitamos el radio, pero el radio es el mismo que el de los demás cuerpos así que no tenemos que volver a medir.
Ya para terminar sumamos el volumen de las tres figuras y el resultado es el volumen total.
Sencillo!!!
De manera igual se hace con todos los cuerpos.