Diferencia entre revisiones de «Algebra de boole»
(→Recuerda) |
|||
| Línea 402: | Línea 402: | ||
1. | 1. | ||
| − | <center>[[archivo:ejemplo3.png|700px|caption]] | + | <center>[[archivo:ejemplo3.png|700px|caption]] |
2. | 2. | ||
| − | <center>[[archivo:ejemplo4.png|900px|caption]] | + | <center>[[archivo:ejemplo4.png|900px|caption]] |
| + | 3. | ||
| + | [[archivo:g4450.png|300px|caption|]] | ||
| + | |||
| + | 4. | ||
| + | |||
| + | [[archivo:g4451.png|300px|caption|]] | ||
| + | |||
| + | </center> | ||
<center><big><big><b>Reflexión</b></big></big></center> | <center><big><big><b>Reflexión</b></big></big></center> | ||
| Línea 419: | Línea 427: | ||
Usar la razón nos lleva a dudar acerca de muchas condiciones a las que nos vemos sometidos diariamente y no nos preguntamos el por que de ellas? Y simplemente aceptamos la realidad tal cual se nos presenta como si fuéramos caballos a los que les ponen su careta bloqueándonos todo el panorama y enseñándonos un solo camino. El uso de la razón y la lógica nos permitirá contestar cualquier pregunta y la que no, se convertirá en un estímulo para vivir. | Usar la razón nos lleva a dudar acerca de muchas condiciones a las que nos vemos sometidos diariamente y no nos preguntamos el por que de ellas? Y simplemente aceptamos la realidad tal cual se nos presenta como si fuéramos caballos a los que les ponen su careta bloqueándonos todo el panorama y enseñándonos un solo camino. El uso de la razón y la lógica nos permitirá contestar cualquier pregunta y la que no, se convertirá en un estímulo para vivir. | ||
| + | |||
| + | |||
| + | |||
Revisión del 12:32 10 feb 2017
La suma, la resta, la multiplicación y división hacen parte de las operaciones aritméticas, las cuales ya hemos estudiado de forma teórica y práctica, pero estás no son las únicas operaciones matemáticas existentes que se encuentran a nuestro alcance, una ellas son lasa flor de piel mientras operaciones booleanas o álgebra de Boole o simplemente lógica y aunque no será presentada a profundidad si veremos algunos conceptos básicos y el surgimiento de esta área de las matemáticas.
El álgebra de Boole se denomina así gracias a George Boole, matemático autodidacta de origen Ingles que fue el primero en proponer el álgebra como parte de un sistema lógico, en otras palabras el álgebra de Boole fue un intento de utilizar técnicas algebraicas para tratar expresiones de forma lógica, de este planteamiento surge un libro importante llamado “ Las leyes del pensamiento ”.

El trabajo de Boole fue tan importante que se aplica de forma generalizada en el ámbito de la electrónica, incluso representa la base de la informática, no únicamente por sus sistema de 1 y 0 (sistema binario) sino también por el desarrollo de circuitos digitales, los lenguajes de programación, los tipos de datos, procesadores, entre otros.




Tal vez no comprendamos aquellas cosas descritas en el párrafo anterior, pero las enunciamos para afirmar el alcance que tuvo el trabajo de Boole si tenemos en cuenta que lo desarrolló en el año 1847 y en la actualidad se sigue usando.
Pese a que esta área de las matemáticas se usa en diversos medios técnicos puede ser de utilidad también para nuestro lenguaje y pensamiento, debido a que la lógica nos permite ordenar de manera racional todas nuestras ideas.
Empecemos a prácticar un poco:
Consideremos dos oraciones sencillas:
1. El sol sale por el oriente
2. La tierra es plana
procedamos a dar valores de Falso y Verdadero
- El sol sale por el oriente: Verdadero
- La tierra es plana: Falso
Conforme se muestra en el ejemplo anterior es posible asignarle a cada oración el valor de Falso o Verdadero, también es posible unir dos diferentes oraciones para formar las llamadas operaciones boolenas.
De nuevo consideremos dos oraciones sencillas:
1. La tierra es esférica
2. La luna tiene un ciclo de 28 días
luego, vamos a definir una operación booleana nombrada “Conjunción” esta es interpretada por la letra “ y “ y nos permite unir dos frases u oraciones.
La tierra es esférica y la luna tiene un ciclo de 28 días
o
La luna tiene un ciclo de 28 días y la tierra es esférica
La operación Conjunción tiene también podemos atribuirle un valor y se hace de la siguiente forma:
- Nombremos a la oración 1. como A y a la oración 2. como B
- La conjunción es Falsa si A es falsa y B verdadera
- La conjunción es Falsa si A verdadera y B falsa
- La conjunción es Falsa si A es falsa y B es falsa
- La conjunción es Verdadera si A es verdadera y B es verdadera
Así, llegamos a la conclusión de que la conjunción solo puede tener el valor de verdad si las dos oraciones que la componen son verdaderas.
Existe otra manera de unir oraciones y es con la operación “ Disyunción “ esta es interpretada por la letra “ o “ ahora, formulemos dos oraciones mas para ejemplificar.
1. Los domingos voy al pueblo
2. Asisto a todas las plenarias
Utilizando la disyunción quedaría:
Los domingos voy al pueblo o asisto a todas plenarias
también
Asisto a todas las plenarias o los domingos voy al pueblo
Al igual que para la operación anterior, la disyunción tiene valores de verdad:
- Nombremos la oración 1. como A y a la oración 2. como B
- La disyunción es Falsa si A es falsa y B es falsa.
- La disyunción es Verdadera si A es verdadera y B es verdadera.
- La disyunción es Verdadera si A es verdadera y B es falsa.
- La disyunción es Verdadera si A es falsa y B es verdadera.
Así, se concluye que la disyunción solo puede ser Falsa si ambas oraciones que la componen son falsas, en el resto de los casos la disyunción es Verdadera, en otras palabras, solo se necesita que una de las dos expresiones sea verdadera para que la operación sea verdadera.
Otra operación booleana es la negación “ no “ que se representa con “ ¬ “ y consiste en cambiar el valor de verdad de una oración o proposición, veamos:
Los rayos siempre viajan de las nubes al suelo
tenemos una oración a la que le asignaremos el valor de Verdadera, además la denominaremos como A.
Entonces si A es Verdadera y aplicamos la negación tendremos:
- A = Verdadera
- ¬A = Falsa
de forma literal sería:
- A = Los rayos siempre viajan de las nubes al suelo
- ¬A = Los rayos no siempre viajan de las nubes al suelo
probemos con una proposición negativa:
No pienso ir a recoger café
la anterior proposición se encuentra en forma negativa, ahora si nombramos a la oración como A y aplicamos la negación:
- A = Falsa
- ¬A = Verdadera
de forma literal sería
- ¬A = No pienso ir a recoger café
- ¬¬A = Pienso ir a recoger café
En las operaciones booleanas la negación no es negar la oración, sino que consiste en cambiar el valor de verdad de la oración, es decir que si tenemos una expresión que es falsa al aplicar la negación, está cambia su valor a verdadera y si la proposición es verdadera al aplicar la negación la oración cambia su valor a falsa.
Iniciando esta unidad nos referimos a las aplicaciones que tiene al álgebra de Boole en nuestra cotidianidad, un ejemplo de ello es la informática, pero antes de profundizar debemos establecer una relación entre los valores de las operaciones booleanas (Falso y Verdadero) y la informática:
- En el álgebra de Boole las proposiciones que hacemos tienen un valor de verdad, estos son o Falso o Verdadero, pero ninguna oración puede tener ambos valores al mismo tiempo.
- En la informática se emplea un sistema de numeración diferente al que usamos nosotros, ese sistema se denomina binario y se compone únicamente por dos números, el 1 y el 0, es decir que las maquinas todo lo escriben con ese par de números, por ejemplo el número 7,289 en binario se escribe 10011001111001. Entonces la forma de relacionar este sistema de numeración y la lógica es asignando los siguientes valores:
- Falso = 0
- Verdadero = 1
y a su vez estas asignaciones se relacionan con la electrónica de la siguiente manera:
- Falso = 0 = Apagado = Sin corriente
- Verdadero = 1 = Encendido = Con corriente
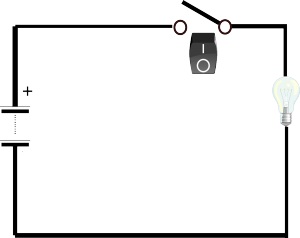
Para ilustrar un poco lo mencionado haremos el próximo ejercicio, vamos a imaginar que tenemos un cable por el cual puede circular corriente eléctrica y además en nuestras manos sostenemos un interruptor o botón que permite o no el paso de la corriente.
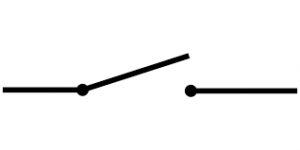
En la figura se puede ver el cable por el que circula corriente, el cual se encuentra incompleto o abierto ¿Que valor tiene este circuito?¿Que valor tendrá al completarlo o cerrarse?
Si el circuito se encuentra abierto no es posible que la corriente circule, por lo tanto el valor que le corresponde en lenguaje maquina es el 0, en el nuestro es Falso. Por el contrario, si el circuito se cierra o se completa la corriente recorre el cable y su valor en este caso sería 1 y/o Verdadero.
Ahora examinemos un circuito con dos interrupotores:
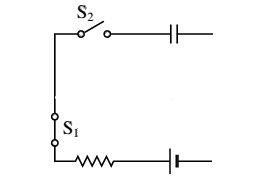
¿Cómo deben permanecer los interruptores para que fluya la corriente?¿Que pasa si solo esta cerrado uno de los circuitos?¿Si esta cerrado el primero y el segundo no, fluye corriente?¿O si esta cerrado el segundo y el primero no, fluye energía?
¿Existe alguna operación booleana que el circuito deba utilizar para que permita dejar pasar la corriente?
En la imagen se visualizan los interruptores como S1 y S2, el primero se encuentra cerrado y el segundo abierto, además si nos fijamos bien, para que la corriente pueda circular ambos interruptores deben permanecer cerrados, por lo que evidentemente la operación que se usa es “ Y “.
Examinemos la siguiente tabla con todas las posibles condiciones:
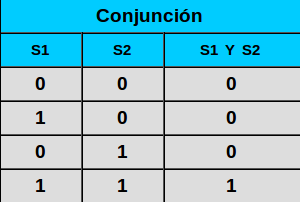
Como se puede observar por los circuitos solo puede pasar corriente cuando ambos tienen valor 1, eso quiere decir deben permanecer cerrados.
Pasemos a mirar un circuito diferente en el que puede utilizarse otra función u operación booleana.
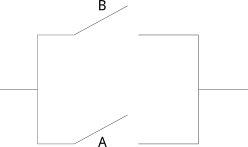
En este caso se observa que la corriente tiene dos caminos a seguir ¿Que pasaría si solo un interruptor esta cerrado?¿Y si los dos están abiertos?
¿Que operación booleana podemos puede implementarse para que fluya la corriente?
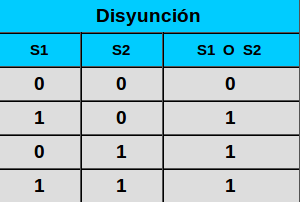
Al examinar la tabla se visibiliza que el valor 0 se arroja como resultado únicamente cuando ambos interruptores son 0, si recordamos la operación “ o “ esta solo es Falsa cuando ambas proposiciones o en este caso interruptores son Falsos.
Ahora ejemplificaremos la última operación vista, “ negación “
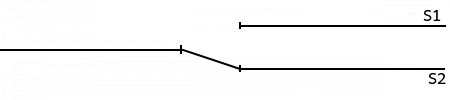
Como en el ejemplo anterior la corriente tiene dos opciones para circular, sin embargo en este circuito solo hay un interruptor (en el otro habían dos), eso quiere decir que la corriente siempre circulará por alguno de los dos cables, el interruptor es para elegir por cual.
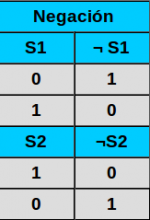
Tenemos el interruptor y dos cables al que puede conectarse, entonces si la primera conexión es de valor 1 o Verdadera, la segunda obligatoriamente es 0 o Falsa, al mover el interruptor cambiamos el camino por el que fluye la corriente, es decir que la conexión dos tiene valor 1 o Verdadero y la primera valor 0 o Falso. Dicho comportamiento es idéntico a la operación booleana “ no “ que recordemos, cambia del valor de las proposiciones y en este caso de las conexiones.
Puertas Lógicas
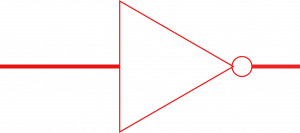
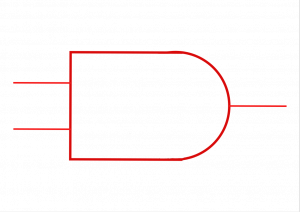
Las operaciones booleanas tienen una representación gráfica para facilitar su implementación a la hora de crear planos para circuitos, estás representaciones son también conocidas como puertas lógicas.
En estas puertas lógicas o representaciones gráficas de las operaciones booleanas, los símbolos varían un poco, por ejemplo la operación " Y " se denotará " A * B ", " AB " o " A . B ", es decir que la operación " Y " se mostrará como un poducto de A y B.
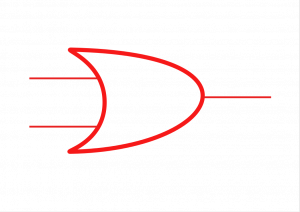
La operación " O " se indica cómo " A + B "
Y la negación " ¬ " será " Ā ".
A continuación veremos una combinación de de puertas lógicas y explicaremos como se trabaja con ellas:
Ejemplo 1
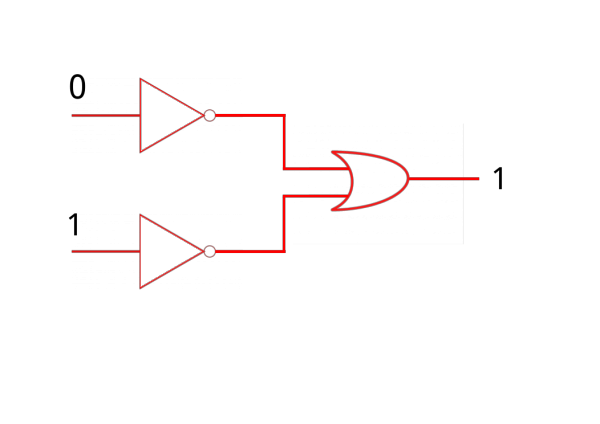
en este ejercicio se nos presentan los símbolos de la disyunción y la negación, también tenemos unas líneas al inicio y final de cada plano las cuales se denominan como "entradas" y "salidas" y en éstas se evidencían los números 0 y 1, lo que corresponde al valor de cada entrada y salida, vale la pena recordar que el 0 y el 1 también se pueden interpretar como Falso y Verdadero o Sin corriente y Con corriente. La forma de operar las puertas lógicas es la siguiente:
Examinando de nuevo el ejercico se observa que en la primera entrada el valor que tiene asignado es 0, luego, siguiendo la línea de la entrada nos encontramos con la puerta lógica que representa la operación booleana de la negación, (recordemos que esta función cambia los valores de verdad) al pasar por dicha puerta el valor 0 se transforma en 1 y continuamos nuestro recorrido hasta la próxima puerta lógica, como ésta requiere de otra operación dejamos ahí para analizar la entrada restante.
La otra entrada tiene asignada el valor 1 y la puerta lógica más cercana es la negación, ahora, al traspasarla cambia el valor de verdad a 0 y continuamos hasta llegar a la puerta de la disyunción; en este punto ya tenemos las dos funciones para analizar dicha puerta. En la primera parte concluimos con 1 y en la segunda con 0, entonces el valor de la salida es de 1. ¿Sabes por qué?
Porque la disyunción tiene valor Falso o 0 cuando ambas proposiciones son Falsas, en este caso tenemos una que tiene valor 0 y otra con valor 1, por lo tanto el resultado nos da 1.
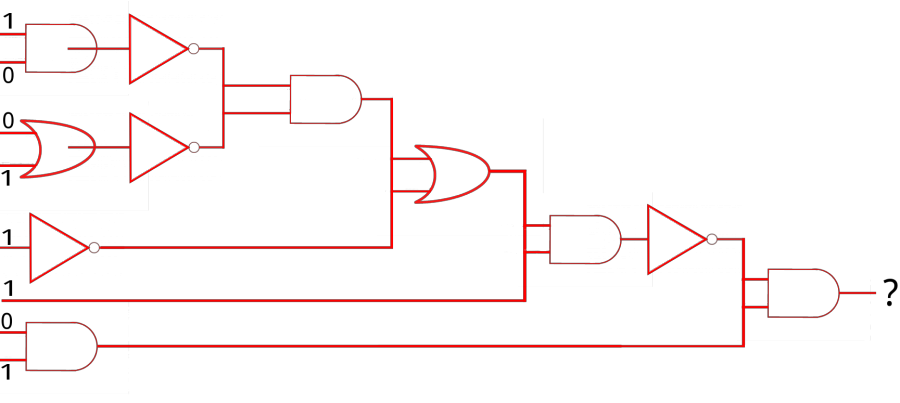
Ejemplo 2:
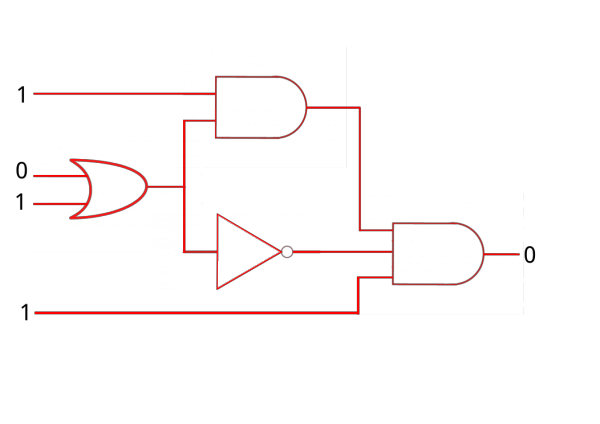
Este parece ser un ejercicio un poco más complicado pero no lo és, solamante tiene más entradas y puertas lógicas, sin embargo la forma de operar es la misma.
Empezamos por las entradas del medio, tienen designado los valores 0 y 1 respectivamente, luego nos encontramos con la puerta lógica de la disyunción, si recordamos la tabla de verdad de ella nos arroja como solución el valor 1, al continuar nos encontramos con una divisón de las líneas del circuito y debemos abordar ambas, trabajemos primero la división superior:
para traspasar la puerta lógica que sigue verificamos la otra entrada que tiene valor de 1, recordemos que la conjunción necesita de dos proposiciones que sean de valor Verdadero para obtener como resultado 1 o Verdadero, si nos fijamos bien la entrada es 1 y la anterior puerta nos arrojo 1 también, por tanto al pasar la conjunción nos da 1, ahora trabajemos la división inferior:
La anterior puerta nos arrojo 1 como solución y la puerta lógica que sigue es la negación, al pasar por ella cambia nuestro valor a 0. Para la última puerta necesitamos tres proposiciones o líneas del circuito, tenemos dos, la tercera la obtenemos de la entrada inferior.
La línea de salida tiene valor 0 debido a que la última puerta es una conjunción y una de las líenas tiene valor 0, por lo tanto es valor general es 0.
Resuelve los siguientes ejercicios:
1.
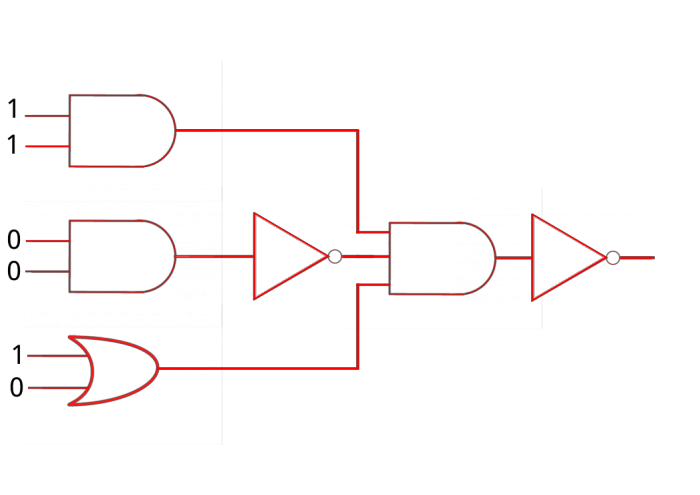
3.
4.
En esta unidad trabajamos acerca de una área de las matemáticas que no emplea gran cantidad de números y operaciones para su estudio, lo que hace que el tema sea un poco menos tedioso que otros, además es la base del funcionamiento de muchas invenciones que se han aplicado en nuestras vidas, son ejemplos la electricidad, la electrónica, la informáticas y de hecho cualquier maquina que requiera circuitos para funcionar. Otra aplicación existente pero menos tangible es la adaptación de la lógica a nuestro pensamiento y en cierto modo menos común también.
Cada vez es más usual ver como el comportamiento de las personas no tiene un sentido en concreto, por ejemplo actuar diferente a como se piensa, esto va contra todo pensamiento razonable. En este punto es donde la lógica entra a jugar un papel importante en nuestras vidas y no me refiero precisamente a hacerlo con operaciones booleanas, sino a pensar por nosotros mismos, a pasar por nuestro razonamiento cada idea que escuchemos o leamos, cada doctrina , cada juicio y cada arquetipo, pues al emplear el razonamiento no solo llegaremos a ser mas inteligentes, lúcidos, capaces, ingeniosos, también seremos más sensibles y más despiertos.
Usar la razón nos lleva a dudar acerca de muchas condiciones a las que nos vemos sometidos diariamente y no nos preguntamos el por que de ellas? Y simplemente aceptamos la realidad tal cual se nos presenta como si fuéramos caballos a los que les ponen su careta bloqueándonos todo el panorama y enseñándonos un solo camino. El uso de la razón y la lógica nos permitirá contestar cualquier pregunta y la que no, se convertirá en un estímulo para vivir.
Recuerda
desarrollaremos actividades complementarias directamente en ZunchoVirtual. Ingresa con el usuario y la contraseña que te dará el/la Tutor/a, una vez dentro busca el Recurso del Grado 6°, allí el curso Multiplicación y división por ultimo Algebra de Boole y desarrolla los ejercicios anteriormente propuestos.