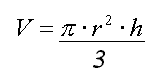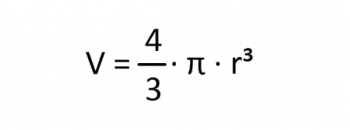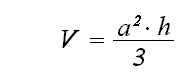Diferencia entre revisiones de «Areas y volumenes»
(→Escala y repaso de conversión de unidades) |
(→Escala y repaso de conversión de unidades) |
||
| Línea 306: | Línea 306: | ||
Con este ejemplo podemos dar una idea intuitiva de lo que es una Escala, pero para ser mas exactos podemos pensar en los planos de una casa o edificio y también en las distancias que aparecen en los mapas, si alguna vez hemos visto un mapa este nos dirá la escala a la cual esta dada la relación con el territorio en la realidad. | Con este ejemplo podemos dar una idea intuitiva de lo que es una Escala, pero para ser mas exactos podemos pensar en los planos de una casa o edificio y también en las distancias que aparecen en los mapas, si alguna vez hemos visto un mapa este nos dirá la escala a la cual esta dada la relación con el territorio en la realidad. | ||
| + | <center>[[Archivo:mapa.jpg|200px|caption]]</center> | ||
| + | |||
| + | ''''Mapa con escala de reducción '''1:250.000''' lo que significa que cada centímetro del mapa son 2.5 Kilometros en la realidad.'''' | ||
Conversión de unidades: | Conversión de unidades: | ||
Revisión del 13:20 21 dic 2016
Contenido
Áreas y Volúmenes por el método de descomposición de cuerpos y figuras
Áreas
Es la superficie que existe dentro de una figura plana (2 dimensiones), también podemos decir que es la porción de tierra que se encuentra delimitada o encerrada por una cerca.
Para medir el área usamos unidades elevadas al cuadrado (m², cm², Km², entre otros).
Repasemos un poco
Cuando estudiamos matemáticas aprendemos las propiedades de un mundo abstracto, de un mundo perfecto, por eso las figuras que contienen ese pedazo de tierra son triángulos, cuadrados, rectángulos, círculos, entre otros.
Ahora si queremos aplicar estas ideas del mundo abstracto al nuestro, encontraremos figuras que no tienen una formula para saber cual es su área, en ese caso podremos separar esa figura de forma extraña a unas figuras mas pequeñas que ya conocemos y con las cuales hemos trabajado con nuestro tutor o compañeros.
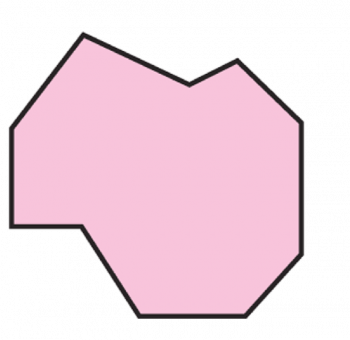
Digamos que tenemos un espacio para hacer piscicultura y tiene la siguiente forma:
para saber cual es el área del estanque debemos separar o descomponerlo en figuras que conozcamos, en este caso podemos ver que nuestro terreno tiene la forma de un Rectángulo y la mitad de un círculo (semi-círculo).
Como ya hemos trabajado con estas figuras antes sabemos que el área de un Rectángulo es bxh y la de un círculo es Pi(r) ² y como es medio círculo lo dividimos en 2, luego el área total es la suma de las áreas que encontramos de forma separada.
En la figura nos indican que la base del Rectángulo mide 19 y la altura 12, ahora si hacemos la separación podemos calcular las áreas por separado y luego sumarlas para hallar el área total:
Sabemos también que la altura del Rectángulo es el diámetro del semi-círculo y que el Radio es la mitad del diámetro:
Altura = Diametro ; (solo para este caso)
Radio = Diametro/2
Radio = 12/2 = 6
Área del semicirculo: Pi(r)² = Pi(6)² ; (recordemos que Pi = 3.14)
Entonces el área total es: área Rectángulo + área semi-círculo:
Ahora analicemos la siguiente figura:
por ejemplo, para esta figura podemos separarla en un semi-círculo, un triangulo y un rectángulo.
Ahora inténtalo con esta:
Recuerda, siempre que tengas que hallar el área de un terreno complicado debes descomponerlo en figuras comunes.
Vídeos sugeridos
https://www.youtube.com/watch?v=JfSHpD9mWCc
https://www.youtube.com/watch?v=wRdvxPOnyM4
Volúmenes
El volumen de un objeto es el espacio que ocupa, también podemos decir que es la capacidad de almacenamiento que tiene. Por ejemplo el volumen de una cubeta es la cantidad de agua que puede almacenar y para medir el volumen usamos unidades elevadas a la 3 (m³, cm³, dm³ , entre otras).
Como vimos antes hay áreas que tienen formas muy complejas para ser medidas, de manera similar hay cuerpos que debemos descomponer en otros cuerpos mas pequeños y conocidos para calcular su volumen. Hagamos un repaso de las figuras comunes:
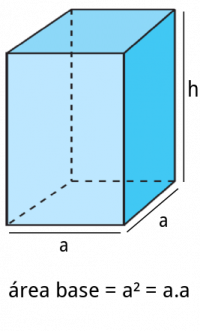
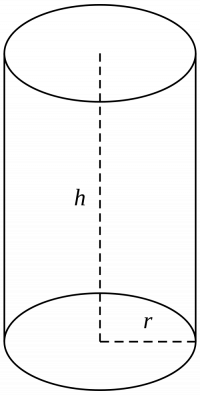
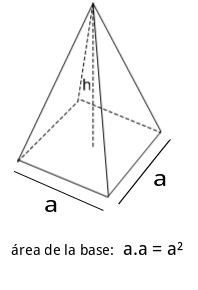
si echamos un vistazo sobre las formulas podemos ver que para todos los cuerpos (menos la esfera), se puede hallar el volumen multiplicando el área de la base y la altura del cuerpo.
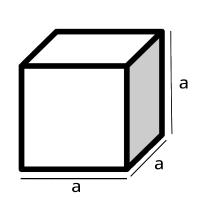
Esta información es muy útil porque el prisma es un caso especial, el prisma puede tener una base en forma de triangulo, cuadrado (como la imagen en este documento), etc.
Por eso para hallar el volumen de un prisma encontramos el área de la base y la multiplicamos por su altura.
Descomposición
Si quisiéramos calcular el volumen de un lápiz únicamente con las anteriores figuras, podríamos hacerlo?

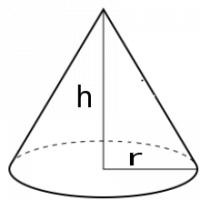
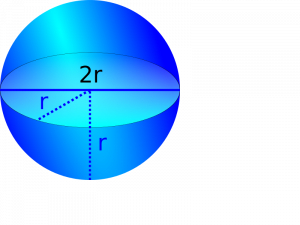
Por supuesto que sí, porque un lápiz como el de la imagen esta construido con un cono (en la punta), un cilindro (la parte de color amarillo) y media esfera (el borrador), así que tenemos que hallar el volumen del cono, del cilindro y la media esfera, para luego sumarla y el resultado es el volumen de todo el lápiz.
Hagamos el ejercicio juntos, toma un lápiz u objeto similar y procedamos:
vamos a separar el lápiz en tres partes, si quieres puedes usar la imaginación o partir un lápiz.
Primero separamos la punta que representa un cono, luego el cilindro y la media esfera que es el borrador.

ahora para hallar el volumen del cono (la punta) medimos su altura h y el radio r y aplicamos la formula.
Para el cilindro necesitamos también un radio r su altura h, pero el radio del cilindro y del cono es el mismo por lo tanto no tenemos que volver a medir el radio.
Para la media esfera solo necesitamos el radio, pero el radio es el mismo que el de los demás cuerpos así que no tenemos que volver a medir.
Ya para terminar sumamos el volumen de las tres figuras y el resultado es el volumen total.
Sencillo!!!
De manera igual se hace con todos los cuerpos.
Vídeo sugeridos
https://www.youtube.com/watch?v=wNVyN30MjZQ
Escala y repaso de conversión de unidades
Miremos un sencillo ejemplo de que es y que representa una escala:
Si observamos el siguiente dibujo podemos decir que su tamaño es de 1 unidad , pero en comparación con el objeto real este estará reducido 10 unidades.

La relación se representa así 1:10 lo que indica que para conocer el tamaño real del objeto debemos multiplicarlo por 10.
Entonces, si el largo del machete en el dibujo mide 10 cm la medida del machete real sera 100 cm.
Así que podríamos decir que una escala es la relación que existe entre las medidas o dimensiones reales de un objeto y las de un dibujo que representa la realidad. Podríamos tomar por Escala como reducir o aumentar el tamaño de un objeto sin que este pierda sus proporciones o la relación que existe entre sus lados en el resultado final.
Por ejemplo:
Supongamos que tenemos una casa en tamaño real (Figura A) y la deseamos escalar de manera que el dibujo ocupe el tamaño de una hoja de cuaderno, el resultado final seria el dibujo a su lado (Figura B).
| Real | Escala |
Como podemos apreciar hemos reducido el tamaño de la casa sin que esta pierda su proporción, podremos decir entonces que hemos escalado la casa.
Con este ejemplo podemos dar una idea intuitiva de lo que es una Escala, pero para ser mas exactos podemos pensar en los planos de una casa o edificio y también en las distancias que aparecen en los mapas, si alguna vez hemos visto un mapa este nos dirá la escala a la cual esta dada la relación con el territorio en la realidad.
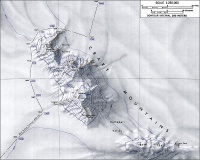
'Mapa con escala de reducción 1:250.000 lo que significa que cada centímetro del mapa son 2.5 Kilometros en la realidad.'
Conversión de unidades: La conversión de unidades es el proceso por medio del cual podemos pasar de una unidad de medida a otra. Por ejemplo podríamos pasar de kilómetros (Km) a su respectivo valor en centímetros (Cm). Longitud: Es una magnitud física, la cual hace referencia a la extensión o a la medida de un objeto en una sola dirección. Factores de conversión:
Múltiplos del metro:
terámetro (Tm): 1012 =1 000 000 000 000 m
gigámetro (Gm): 109 = 1 000 000 000 m
megámetro (Mm): 106 = 1 000 000 m
kilómetro (km): 103 = 1,000 m
hectómetro (hm): 102 =100 m
decímetro (dm): 10-1 metros ó 1m = 10 dm
centímetro (cm): 10-2 metros ó 1m = 100 cm
milímetro (mm): 10-3 metros ó 1m = 1000 mm
angstrom (Å): 10-10 metros ó 1m = 100000000 Å
Masa:
Hemos definido como materia todo aquello que tiene masa y ocupa un lugar en el espacio. En el sistema métrico, las unidades utilizadas para medir la masa son, normalmente, los gramos, kilogramos o miligramos.
1 Kg = 1000 g
1 g = 1000 mg
1 Ton = 1000 Kg
1 Lib = 453.6 g
1 Kg= 2.2 lib
1 arroba = 25 lib
I oz= 28 g
UNIDADES DE TIEMPO Y CONVERSIONES
1 h= 60 min = 3600 seg
1 min = 60 seg
1 día= 24 h = 1440 min= 86400 seg
1 semana= 7 dias
1 año= 52 semanas= 12 meses= 365 días
1 década = 10 años
1 siglo= 100 años
1 milenio = 1000 años
LA TEMPERATURA
Es una propiedad de la materia que está relacionada con la sensación de calor o frío que se siente en contacto con ella.

EL VOLUMEN:
El volumen de un objeto es el espacio que ocupa, también podemos decir que es la capacidad de almacenamiento que tiene. Por ejemplo el volumen de una cubeta es la cantidad de agua que puede almacenar y para medir el volumen usamos unidades elevadas a la 3 (m³, cm³, dm³ , entre otras).
1 m3 = 1 000000 cm3
1 m3= 1000 dm3
1 m3= 1000 l
1 l = 1 dm3
1 ml= 1 cm3
1 galón = 3.785 l
1 botella= 780 ml
1 cucharada= 5 ml
1 l = 1000 ml = 1000cm3
Ejemplo 1: -Digamos que Pedro recorre 3 Km desde su finca hasta el lugar donde estudia y desea saber cuanto son 3 Km en centímetros, Para esto recurre a la conversión de unidades.
Primero pone lo que desea convertir: 3 Km
en este caso, primero se debe pasar de kilómetros a metros (m), tenemos que 1 km equivale 1000 m luego este será el factor de conversión así que multiplicará los 3 Km por una fracción 1000m/1 Km donde el denominador será las unidades a cancelar y en el numerador su equivalente en la unidad a la que lo desea llevar.
3 Km * 1000m/1 Km = ? (recordar multiplicación de fraccionarios)
operando tendríamos que: cancelamos los Km con Km y multiplicamos 3*1000 m lo que seria igual a 3000 m. como Pedro desea llegar a centímetros ahora se deberán pasar los 3000 m a centímetros, teniendo en cuenta que el factor de conversión en esta ocasión cambia puesto que 1 m son 100 cm, esta vez el procedimiento quedaría así:
3000 m * 100cm/1m
ahora cancelamos metros con metros y multiplicamos 3000 * 100 cm lo que sera igual a 300.000 cm. Después de esta conversión Pedro se da cuenta que los 3 km que recorre desde su finca hasta el lugar donde estudia también son 300.000 cm pero no solo podemos hacer conversiones entre medidas de longitud también podemos realizar conversiones entre unidades de volumen. -supongamos que deseamos convertir 5 metros cúbicos (m³) a centímetros cúbicos (cm³) primero debemos tener en cuenta que 1 m son 100 cm si estamos hablando de unidades de longitud, pero ya que hablaremos de unidades de volumen debemos elevar esta fracción al cubo osea (100 Cm/1 m)³ lo que es igual a:
(100cm)³ = 1'000'000 cm ³
(1 m)³ = 1 m³ lo que nos quedaría seria:
5 m³ * 1'000'000 cm ³/1 m³ =?
se cancelan m³ con m³ y procedemos a operar 5*1'000'000 Cm³ divido entre 1 el resultado final es igual 5'000'000 Cm³.
La conversión de unidades a la hora de hacer una escala: Ya que a la hora de hacer un objeto a escala no nos podemos dejar llevar por la intuición ya que el objeto escalado debe ser exacto o en su defecto lo mas aproximado con la realidad es acá donde entra la conversión de unidades.
Ejemplo 1
Digamos que un joven desea hacer una maqueta a escala del edificio Coltejer ubicado en la ciudad de medellín el cual tiene una altura de 175 m desde su base hasta la ultima punta del edificio, el joven desea que el dibujo inicial para la maqueta le quede con una altura del tamaño de una hoja de papel la cual tiene una altura de 25 Cm, el joven desea saber cual es la relación que hay entre la hoja y el edifico para así poder escalar los demás lados del edificio.
- Debido a que si se trabaja con las unidades de metros y centímetros no se podrá obtener el resultado correcto, primero se debe hacer la conversión de unidades bien sea de la altura del edificio a centímetros o la altura de la hoja a metros, en este caso convertiremos la altura del Coltejer a Cm de la siguiente manera:
175,00 m * 100 Cm / 1 m = 17500 Cm
- luego para obtener la relación de la escala entre las dos alturas haremos lo siguiente:
17500 Cm / 25 Cm = 700