Diferencia entre revisiones de «Areas y volumenes»
(→Áreas) |
(→Áreas y Volúmenes por el método de descomposición de cuerpos y figuras) |
||
| Línea 85: | Línea 85: | ||
===Ejercicios=== | ===Ejercicios=== | ||
| − | + | ''Hallar el área de los siguientes terrenos:'' | |
Revisión del 18:39 11 nov 2016
Contenido
Áreas y Volúmenes por el método de descomposición de cuerpos y figuras
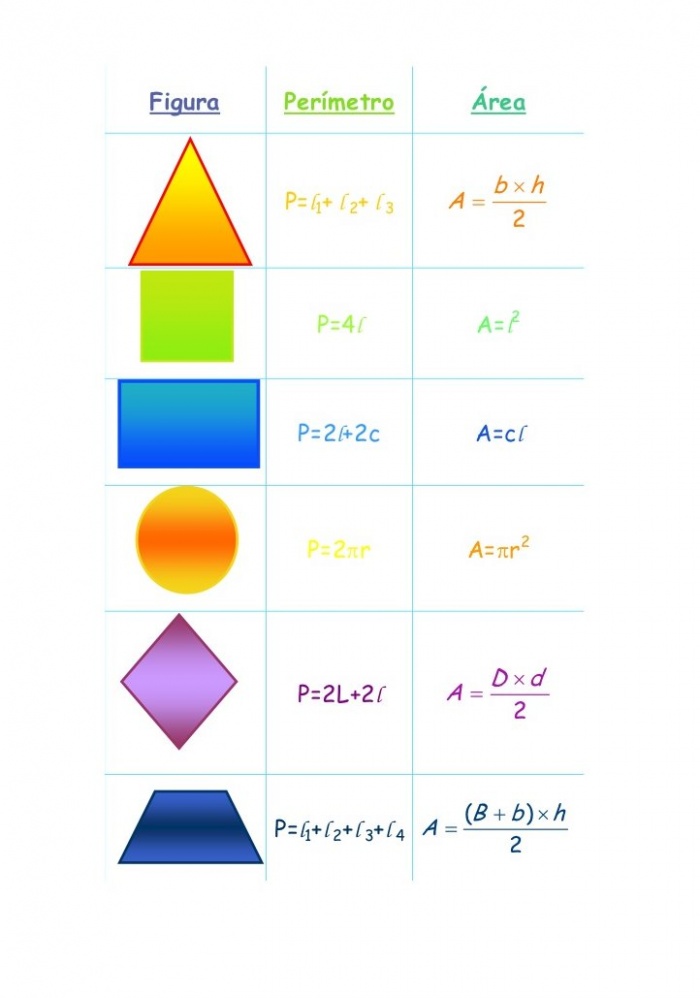
Áreas
Es la superficie que existe dentro de una figura plana (2 dimensiones), también podemos decir que es la porción de tierra que se encuentra delimitada o encerrada por una cerca.
Para medir el área usamos unidades elevadas al cuadrado (m², cm², Km², entre otros).
Repasemos un poco
Cuando estudiamos matemáticas aprendemos las propiedades de un mundo abstracto, de un mundo perfecto, por eso las figuras que contienen ese pedazo de tierra son triángulos, cuadrados, rectángulos, círculos, entre otros.
Ahora si queremos aplicar estas ideas del mundo abstracto al nuestro, encontraremos figuras que no tienen una formula para saber cual es su área, en ese caso podremos separar esa figura de forma extraña a unas figuras mas pequeñas que ya conocemos y con las cuales hemos trabajado con nuestro tutor o compañeros.
Digamos que tenemos un espacio para hacer piscicultura y tiene la siguiente forma:
para saber cual es el área del estanque debemos separar o descomponerlo en figuras que conozcamos, en este caso podemos ver que nuestro terreno tiene la forma de un Rectángulo y la mitad de un círculo (semi-círculo).
Como ya hemos trabajado con estas figuras antes sabemos que el área de un Rectángulo es bxh y la de un círculo es Pi(r) ² y como es medio círculo lo dividimos en 2, luego el área total es la suma de las áreas que encontramos de forma separada.
En la figura nos indican que la base del Rectángulo mide 19 y la altura 12, ahora si hacemos la separación podemos calcular las áreas por separado y luego sumarlas para hallar el área total:
Sabemos también que la altura del Rectángulo es el diámetro del semi-círculo y que el Radio es la mitad del diámetro:
Altura = Diametro ; (solo para este caso)
Radio = Diametro/2
Radio = 12/2 = 6
Área del semicirculo: Pi(r)² = Pi(6)² ; (recordemos que Pi = 3.14)
Entonces el área total es: área Rectángulo + área semi-círculo:
Ahora analicemos la siguiente figura:
por ejemplo, para esta figura podemos separarla en un semi-círculo, un triangulo y un rectángulo.
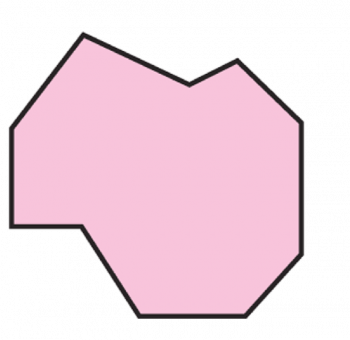
Ahora inténtalo con esta:
Recuerda, siempre que tengas que hallar el área de un terreno complicado debes descomponerlo en figuras comunes.
Ejercicios
Hallar el área de los siguientes terrenos: