Diferencia entre revisiones de «Figuras tridimensionales»
| Línea 3: | Línea 3: | ||
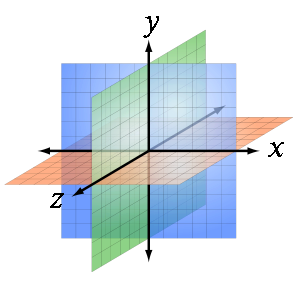
Según el módulo de propiedades las figuras que tu dibujas en una hoja de papel son bidimensionales, mientras que un objeto es tridimensional si tiene tres dimensiones. Es decir, cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. Por ejemplo, anchura, longitud y profundidad. | Según el módulo de propiedades las figuras que tu dibujas en una hoja de papel son bidimensionales, mientras que un objeto es tridimensional si tiene tres dimensiones. Es decir, cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. Por ejemplo, anchura, longitud y profundidad. | ||
| − | + | [[Archivo:ejes_x_y_z.png|500px|caption|center]] | |
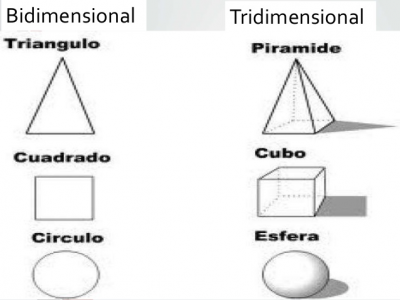
Aunque una superficie plana tiene dos dimensionales, podemos dibujar en ellas objetos tridimensioales. A continuación se representan en forma bidimensional y tridimensional, las figuras geométricas más conocidas por todos nosotros. | Aunque una superficie plana tiene dos dimensionales, podemos dibujar en ellas objetos tridimensioales. A continuación se representan en forma bidimensional y tridimensional, las figuras geométricas más conocidas por todos nosotros. | ||
| − | + | [[Archivo:bidi_tridi.png|400px|caption|center]] | |
| Línea 23: | Línea 23: | ||
[[Archivo:34.png|200px|caption|center]] | [[Archivo:34.png|200px|caption|center]] | ||
| − | Cilindro | + | *Cilindro |
[[Archivo:35.png|200px|caption|center]] | [[Archivo:35.png|200px|caption|center]] | ||
| − | Cono | + | *Cono |
Introducción | Introducción | ||
| Línea 48: | Línea 48: | ||
Como puedes ver, la vista en perspectiva luce más “real” al ojo, pero en geometría, las representaciones en isométrico son útiles para medir y comparar distancias. | Como puedes ver, la vista en perspectiva luce más “real” al ojo, pero en geometría, las representaciones en isométrico son útiles para medir y comparar distancias. | ||
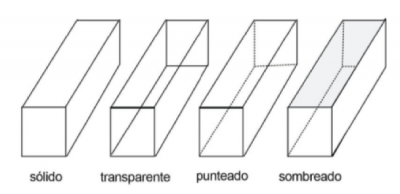
A la vista en isométrico con frecuencia se le muestra en una forma transparente o forma “ver a través”. | A la vista en isométrico con frecuencia se le muestra en una forma transparente o forma “ver a través”. | ||
| + | |||
| + | [[Archivo:38.png|400px|caption|center]] | ||
| + | |||
| + | Color y sombras también pueden ser agregadas para ayudar al ojo a visualizar el sólido. | ||
| + | |||
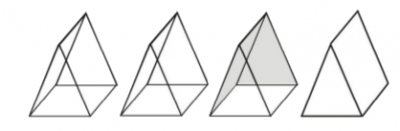
| + | Ejemplo 1 | ||
| + | Mostrar vistas en isométrico de un prisma con una base triangular. | ||
| + | |||
| + | [[Archivo:39.png|400px|caption|center]] | ||
| + | |||
| + | Ejemplo 2 | ||
| + | Mostrar una vista en isométrico en forma transparente de un prisma con una base hexagonal. | ||
| + | |||
| + | [[Archivo:40.png|400px|caption|center]] | ||
| + | |||
| + | Vista ortográfica | ||
| + | |||
| + | Una proyección ortográfica es una vista al vuelo de un sólido que muestra una representación plana de cada uno de los lados de las figuras. Una buena forma de ver cómo trabaja una proyección ortográfica es construir una. El poliedro no convexo mostrado tiene una proyección diferente en cada lado. | ||
| + | |||
| + | [[Archivo:42.png|400px|caption|center]] | ||
| + | |||
| + | Para mostrar la figura en una vista ortográfica, colócala en una caja imaginaria. | ||
| + | |||
| + | [[Archivo:42.png|400px|caption|center]] | ||
| + | |||
| + | Ahora proyecta hacia afuera cada una de las paredes en la caja. Tres de estas vistas se muestran abajo. | ||
| + | |||
| + | [[Archivo:43.png|400px|caption|center]] | ||
| + | |||
| + | Una vista ortográfica al vuelo más completa muestra la imagen del lado en cada una de las seis paredes de la caja. | ||
| + | |||
| + | [[Archivo:44.png|400px|caption|center]] | ||
| + | |||
| + | La misma imagen luce como esto en una vista desplegable. | ||
Revisión del 22:00 12 nov 2016
Figuras Tridimensionales
Según el módulo de propiedades las figuras que tu dibujas en una hoja de papel son bidimensionales, mientras que un objeto es tridimensional si tiene tres dimensiones. Es decir, cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. Por ejemplo, anchura, longitud y profundidad.
Aunque una superficie plana tiene dos dimensionales, podemos dibujar en ellas objetos tridimensioales. A continuación se representan en forma bidimensional y tridimensional, las figuras geométricas más conocidas por todos nosotros.
Paralelepipedo
Prisma triangular
- Cilindro
- Cono
Introducción La mejor forma de representar una figura tridimensional es usar un modelo del sólido. Desafortunadamente, los modelos algunas veces no están disponibles. Existen cuatro formas primarias de representar sólidos en dos dimensiones sobre el papel. Estas son:
Una vista en isométrico (o perspectiva). Una vista ortográfica o al vuelo . Una vista en sección transversal. Una red (malla).
Vista en isométrico
La típica vista tridimensional de un sólido es la vista en isométrico . Estrictamente hablando, una vista en isométrico de un sólido no incluye perspectiva. La perspectiva es la ilusión usada por artistas para hacer que las cosas aparezcan más pequeñas en la distancia que las cosas cercanas usando un punto de fuga donde convergen las líneas paralelas.
Las figuras de abajo muestran la diferencia entre una vista en isométrico y una vista en perspectiva de un sólido.
Como puedes ver, la vista en perspectiva luce más “real” al ojo, pero en geometría, las representaciones en isométrico son útiles para medir y comparar distancias. A la vista en isométrico con frecuencia se le muestra en una forma transparente o forma “ver a través”.
Color y sombras también pueden ser agregadas para ayudar al ojo a visualizar el sólido.
Ejemplo 1 Mostrar vistas en isométrico de un prisma con una base triangular.
Ejemplo 2 Mostrar una vista en isométrico en forma transparente de un prisma con una base hexagonal.
Vista ortográfica
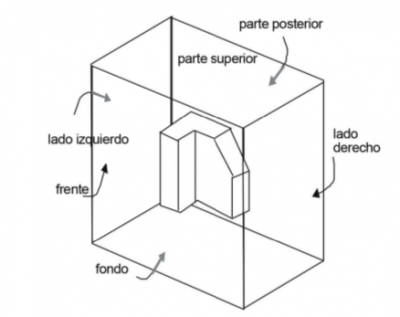
Una proyección ortográfica es una vista al vuelo de un sólido que muestra una representación plana de cada uno de los lados de las figuras. Una buena forma de ver cómo trabaja una proyección ortográfica es construir una. El poliedro no convexo mostrado tiene una proyección diferente en cada lado.
Para mostrar la figura en una vista ortográfica, colócala en una caja imaginaria.
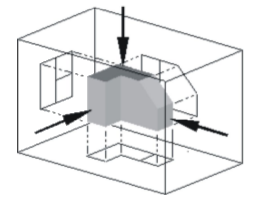
Ahora proyecta hacia afuera cada una de las paredes en la caja. Tres de estas vistas se muestran abajo.
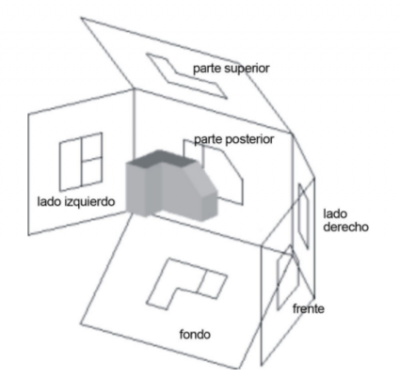
Una vista ortográfica al vuelo más completa muestra la imagen del lado en cada una de las seis paredes de la caja.
La misma imagen luce como esto en una vista desplegable.