Diferencia entre revisiones de «Division»
| Línea 165: | Línea 165: | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Línea 214: | Línea 197: | ||
208 / 4 = | 208 / 4 = | ||
360 / 3 = | 360 / 3 = | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| + | Puede que en algún momento nos encontremos con un numero divido por 10, 100, 1000... también puede que pienses que para resolver esas divisiones tienes que usar calculadora, pero no es así, lo único que tendremos que hacer es contar desde las Unidades y hacia la izquierda tantas posiciones como ceros tenga el número que divide y al haber terminado colocamos una coma para indicar que el resultado es un número decimal. | ||
| + | |||
| + | |||
| + | <center> | ||
| + | |||
| + | Por ejemplo : 435 / 10 = 43,5 | ||
| + | |||
| + | 435 /100 = 4, 35 | ||
| + | </center> | ||
| + | |||
| + | |||
| + | Conforme nos indican las instrucciones el número que divide es el 10 y este solo tiene un cero; ahora nos ubicamos en las Unidades y nos desplazamos a las Decenas y ubicamos la coma que nos indica que el número es decimal. | ||
| + | |||
| + | En el segundo ejemplo el número que divide es el 100 y como este tiene dos ceros, entonces no ubicamos en las Unidades y nos desplazamos dos posiciones hacia la izquierda quedando en las Centenas y luego ponemos la coma para indicar que es un decimal. | ||
| + | |||
| + | |||
| Línea 248: | Línea 248: | ||
| − | Realice las siguientes divisiones | + | Realice las siguientes divisiones: |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | <center> | ||
| + | {| border="1" style="background:#3780" align="top" class="sortable wikitable"" | ||
| + | |547 / 100 = | ||
| + | |- | ||
| + | |10,5 / 10 = | ||
| + | |- | ||
| + | |100 / 100 = | ||
| + | |- | ||
| + | |4569,76 / 10= | ||
| + | |- | ||
| + | |5 / 100 = | ||
| + | |- | ||
| + | |50 / x = 5 | ||
| + | |} | ||
| + | </center> | ||
- alguna vez puede que tengamos que trabajar con expresiones similares a esta 460 / 20, lo que se hará para simplificar aún mas la división será quitar una cantidad igual de ceros de cada lado así quedará 46 / 2 = 23 o 400 / 1000 en este caso podemos quitar dos ceros a cada lado, pero ya no se es posible quitar tres, así lo que nos quedaría del ejemplo anterior es 4 / 10 = 0,4. Además recuerde que para poder eliminar ceros estos deben estar al final del número no entre otros número diferentes a el; Practique con los siguientes ejercicios. | - alguna vez puede que tengamos que trabajar con expresiones similares a esta 460 / 20, lo que se hará para simplificar aún mas la división será quitar una cantidad igual de ceros de cada lado así quedará 46 / 2 = 23 o 400 / 1000 en este caso podemos quitar dos ceros a cada lado, pero ya no se es posible quitar tres, así lo que nos quedaría del ejemplo anterior es 4 / 10 = 0,4. Además recuerde que para poder eliminar ceros estos deben estar al final del número no entre otros número diferentes a el; Practique con los siguientes ejercicios. | ||
Revisión del 17:01 7 feb 2017
¿Qué es la división?:
Cómo la palabra lo indica, división es partir, repartir o distribuir un conjunto de elementos en partes iguales, por lo tanto la división es el resultado de una repartición equitativa o igualitaria.
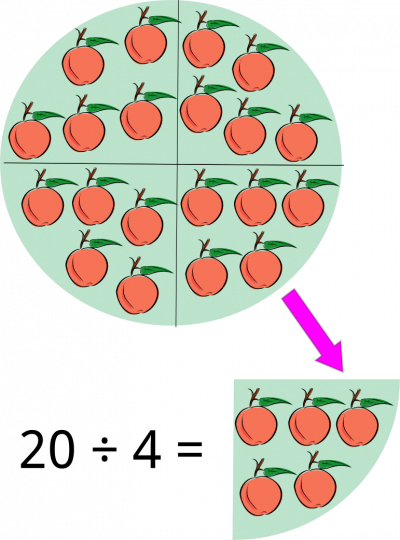
En la siguiente imagen se ilustra un conjunto de manzanas, en total 20 manzanas ubicadas de tal forma que al dividirlas en 4 partes iguales nos quedan 5 manzanas en cada parte.
Como la división es una repartición igualitaria podemos abordar este problema de la siguiente forma.
Entre tres amigos y yo recogemos 20 manzanas y al realizar la distribución igualitaria o división cada uno queda con 5 manzanas.
Ahora examinemos lo que pasa con jennifer:
Jennifer junto con su familia viven en una vereda, para su sustento se dedican a la agricultura y su principal actividad es el cultivo de cacao, además se encargan de su transformación. Jennifer cada domingo con su padre salían a vender el chocolate a una tienda del pueblo, su padre le vende al tendero 5 libras de chocolate. Un día jennifer se da cuenta que el señor de la tienda divide el chocolate en cuartos, y cada cuarto lo fracciona en 8 pares de pastas mas pequeñas y los vende a las demás personas. A jennifer esto le parece una excelente idea pues no todas las personas necesitan todo el cuarto de libra y así ella podría hacer lo mismo que el señor de la tienda y vender unos cuantos cuartos de chocolate por pastas y ayudar un poco con el sustento de su hogar sin dejar de estudiar.
Jennifer muy entusiasmada decide contarle a su padre lo que se le ocurrió y él le pregunta:
<< ¿Cuanto costarán?>>
Jennifer se queda pensando y al cabo de un tiempo le pregunta a su padre:
<< ¿Cuánto cuesta un solo cuarto de libra de chocolate? >>
a lo que él responde:
<< considero que puede valer unos 5200$>>
<< Entonces es sencillo, las venderemos a 650$ >>
Su padre se queda asombrado pues le sorprende mucho las capacidades de su hija.
A la siguiente semana jennifer se encarga de partir un cuarto de libra en pastas mas pequeñas para venderlas en el colegio.

Miremos la conversación que jennifer sostuvo con su papá. En un momento, ella hizo unos cálculos mentales. ¿Qué era lo que trataba de resolver? ¿Cómo supo ella el costo del par de pastas de chocolate con la información que le dio su papá?
Miremos lo que jennifer hizo:
su padre le dijo que el cuarto de libra cuesta $5200 y ella sabe puede dividir el cuarto de libra de su chocolate 8 pares de pastas o lo que es lo mismo en 16 pedazos, así con el conocimiento que ha adquirido gracias a su autoestudio sabe que 5200 es igual a multiplicar 8 por el por el precio de cada par, lo que sería una pequeña ecuación así:
y c es el precio de cada par de pastas, ¿acaso no se es muy difícil intentar multiplicar una gran cantidad de números por 8 hasta encontrar uno que de 5200?, así que Jennifer después de pensarlo mejor decidió que el precio de todo el cuarto de libra de chocolate dividido por el número de pares de pastas contenidas en él, deberia dar el precio de un cuarto de libra de chocolate. Así que esto se puede escribir así:
c = 5200 ÷ 8
c = 650 $
Y si quiere saber el precio de los 16 pedazos solo debe dividir el precio del cuarto de libra entre 16
c = 5200 ÷ 16
c = 325
si dividimos el valor de cada pasta entre 2 nos da el resultado anterior
Ya sabemos que c = 650$, lo que quiere decir que 5200 ÷ 8 = 650. según lo que acabamos de hacer, es claro que la división es la operación inversa a la multiplicación. Cuando dividimos 5200 por 8, por ejemplo, lo que en verdad estamos preguntando es, «por que número podemos multiplicar el 8 para que nos de 5200?». Por lo tanto podemos decir que :
5200 ÷ 8 = 650 es lo mismo que 5200 = 8 x 650
Así que como podemos darnos cuenta que una regla sería
a / b = c " lo que sería igual a " a = b x c
tal parece ya nos familiarizamos con el símbolo que hemos utilizado todo este tiempo para representar la división. ¿habrá otro símbolo que también represente la división entre dos números?
La respuesta es si, tal símbolo es / ; por ejemplo, 16 ÷ 4 = 4 es lo mismo que 16 / 4 = 4.
Ya que se tiene claro que la división es lo contrario a la multiplicación, llene los espacios en
blanco en el siguiente ejercicio.
| 30 ÷ 5 = 30 / 5 = 6 | es igual a 30 = 6 × 5 |
| 14 ÷ 7 = 14 / 7 = | es igual a 14 = ______ × 2 |
| 22 ÷ 2 = 22 / 2 = 11 | es igual a =______ × ______ |
| 36 ÷ 4 = ______ = | es igual a =______ × ______ |
| 28 ÷ 7 = ______ = | es igual a = ______ × ______ |
| 35 ÷ 5 = ______ = | es igual a =______ × ______ |
| 14 ÷ 1 = ______ = | es igual a =______ × ______ |
si 50 ÷ 2 = 25. ¿Es cierto también que 50 ÷ 25 = 2 ? indaguemos la respuesta a esta pregunta llenando los espacios que aparecen a continuación.
Propiedad distributiva:
Para dividir es posible también aplicar la propiedad distributiva de la multiplicación:
- lo primero que debes hacer es descomponer el número que vamos a dividir de forma aditiva, es decir a reescribirlo como si fuera una suma.
- luego debes dividir cada sumando por el divisor.
- por último sumar los cocientes o resultados obtenidos.
Ejemplo: 96 ÷ 3.
96 = 90 + 6 = (90 + 6) ÷ 3
= (90 ÷ 3) + (6 ÷ 3) 30 + 2 = 32
Utilizando el método anterior resuelva las siguientes divisiones:
108 / 4 =
208 / 4 =
360 / 3 =
Puede que en algún momento nos encontremos con un numero divido por 10, 100, 1000... también puede que pienses que para resolver esas divisiones tienes que usar calculadora, pero no es así, lo único que tendremos que hacer es contar desde las Unidades y hacia la izquierda tantas posiciones como ceros tenga el número que divide y al haber terminado colocamos una coma para indicar que el resultado es un número decimal.
Por ejemplo : 435 / 10 = 43,5
435 /100 = 4, 35
Conforme nos indican las instrucciones el número que divide es el 10 y este solo tiene un cero; ahora nos ubicamos en las Unidades y nos desplazamos a las Decenas y ubicamos la coma que nos indica que el número es decimal.
En el segundo ejemplo el número que divide es el 100 y como este tiene dos ceros, entonces no ubicamos en las Unidades y nos desplazamos dos posiciones hacia la izquierda quedando en las Centenas y luego ponemos la coma para indicar que es un decimal.
¿Y si el número que divide es mayor?
Sin importar que eso pase el procedimiento a seguir es el mismo, contamos los ceros que tenga el divisor y nos desplazamos según el número de ceros y como el divisor es mayor hay más ceros que posiciones, aparentemente no es posible continuar, sin embargo podemos hacerlo si ubicamos un cero, luego podemos seguir moviéndonos y el se repite hasta que se han contado todos los ceros del divisor y por último no debemos olvidar ubicar la coma para indicar que es decimal.
El número 435 esta siendo dividido por 10000, este tiene cuatro ceros y debemos movernos desde las Unidades pasando por las Decenas, Centenas, Unidades de mil, la cual esta vacía y ubicando un cero podemos proseguir a las Decenas de mil que también se encuentra vacía, por lo tanto ubicamos otro cero; y en este punto ya nos hemos movido cuatro espacios y el divisor tiene cuatro ceros, es decir que hemos terminado, solo falta ubicar la coma que indica decimal para obtener la solución.
Con los decimales ocurre de forma similar y como ellos ya tienen una coma solo es necesario desplazarla según el número de ceros del divisor.
Por ejemplo: 670,5 /10 = 67,05
670,5 / 1000 = 0,6705
Por ejemplo 35000 / 100 = 350
Realice las siguientes divisiones:
| 547 / 100 = |
| 10,5 / 10 = |
| 100 / 100 = |
| 4569,76 / 10= |
| 5 / 100 = |
| 50 / x = 5 |
- alguna vez puede que tengamos que trabajar con expresiones similares a esta 460 / 20, lo que se hará para simplificar aún mas la división será quitar una cantidad igual de ceros de cada lado así quedará 46 / 2 = 23 o 400 / 1000 en este caso podemos quitar dos ceros a cada lado, pero ya no se es posible quitar tres, así lo que nos quedaría del ejemplo anterior es 4 / 10 = 0,4. Además recuerde que para poder eliminar ceros estos deben estar al final del número no entre otros número diferentes a el; Practique con los siguientes ejercicios.
2300 / 10 =
600000 / 8000 =
690 / 30 =
4500 / 600 =
500 / 20 =
280 / 70 =
21500 /4000=
3500 / 50 =
6600 / 110 =
- Ahora aprendamos a hacer divisiones por números específicos como lo son el 5 y el 4, cuando vaya a dividir un número entre 5 lo único que se debe hacer es multiplicar el dividendo por dos y luego de esto dividirlo entre 10 por ejemplo 65 / 5, primero 65 x 2 = 130 luego de esto 130 / 10 = 13 o 160 / 5 repetimos el procedimiento 160 x 2 = 320 y 320 / 10 = 32. Miremos que pasa cuando la división es por el 4, para dividir entre 4 lo que se tiene que hacer es simplemente dividir dos veces entre dos, supongamos que debemos dividir 32 / 4, dividimos entre dos 32 / 2 = 16 y repetimos el procedimiento 16 / 2 = 8, así el cociente será 8. Es importante que recuerde que en alguna ocasiones le puede dar decimal, por ejemplo si dividimos 22 /4 y hacemos el procedimiento 22 / 2 = 11 y 11 /2 = 5.5, repasemos con el siguiente ejercicio:
60 ÷ 4 =
208 ÷ 4 =
44 ÷ 4 =
23 ÷ 5 =
68 ÷ 5 =
150 ÷ 5 =
200 ÷ 4 =
58 ÷ 4 =
128 ÷ 4 =
210 ÷ 5 =
0.8 ÷ 5 =
265 ÷ 5 =
208 ÷ 4 =
44 ÷ 4 =
23 ÷ 5 =
68 ÷ 5 =
150 ÷ 5 =
200 ÷ 4 =
Hablemos sobre la división :
Constantemente nuestra vida está regida por distintas operaciones matemáticas, sumamos personas a grandes empresas, sumamos productos a la canasta familiar, aumentan los precios de la vida, a las distintas entidades de gobierno se suman nuevas personalidades que asumen los cargos de poder y con esto se resta la calidad de vida de los habitantes de municipios, ciudades, departamentos y finalmente países. Se resta la calidad del aire y disminuye la salud de todas las personas que dedican su vida a a producir y a sumar las ganancias de grandes emporios a quienes no les interesa multiplicar el bienestar físico y o emocional de quienes en cambio si les ayudan multiplican sus ganancias.
Finalmente podemos decir que está la división si vivimos en una sociedad en la que hasta la persona que permanece sin vida en la penumbra de un ataúd, necesita vestido, transporte es totalmente necesario que hayan otras personas que cumplan con la labor de conducir el automóvil con el féretro y también el que fabrique el ultimo vestido que usara aquel occiso. Hay otras personas que cultivan pues no hay persona viva que no sienta deseos de saciar su apetito con un buen festín. Así infinidad de tareas que existen para poder satisfacer las necesidades para la vida de los seres humanos pues es justo que cada persona escoja cual de estas tareas quiere realizar; A todo esto se le llama división del trabajo y consiste en que cada persona desde sus habilidades y capacidades pueda contribuir al desarrollo de la sociedad desde el campo que mas capte su atención, pero también es justo que haya una correcta división de todos los bienes materiales e inmateriales que miles de personas producen a diario pues la sociedad actual no cumple con la regla de la división y es lograr repartir cada parte por igual, a lo que se hace referencia es que unos pocos pueden estudiar por su posición económica mientras otros siempre deberán trabajar para quizás algún día llegar a hacerlo, no hay una correcta división cuando una persona se muere por no trabajar durante su vida pues siempre tuvo la facilidad económica para darse aquel lujo mientras hayan otros que fallezcan por trabajar demasiado, con todo esto solo queda una pregunta o tal vez muchas, pero la que destaca es ¿ En donde está la división equitativa e igualitaria en los distintos campos de nuestra vida y en la sociedad?.
