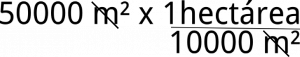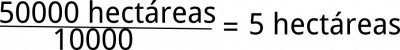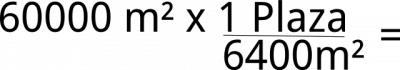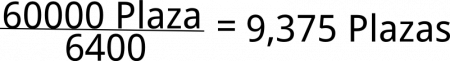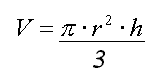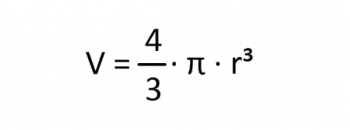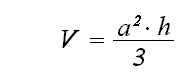Diferencia entre revisiones de «Areas y volumenes»
| Línea 278: | Línea 278: | ||
<hr noshade> | <hr noshade> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<center>[[Archivo:Path3021.png|300px|caption|]]</center> | <center>[[Archivo:Path3021.png|300px|caption|]]</center> | ||
Revisión del 18:50 6 feb 2017
Usualmente solemos escuchar las palabras “área” y “volumen” ¿a qué se refieren con estos términos?, ¿cómo se emplean?, ¿donde se emplean? La idea de esta unidad es que comprendamos estos dos conceptos y así aplicarlos en nuestra vida cotidiana.
El área se puede definir como la superficie de una figura , imaginemos un terreno cercado, todo lo que este dentro de la cerca será su área, en cambio lo que este por fuera de esta ya no hará parte del área. Es importante tener en cuenta sus unidades por ejemplo cm², m², km² ….
Supongamos que deseamos saber el área de un terreno el cual tiene medidas de 6 u de largo y 6 u de ancho. Tenga en cuenta que la u son unidades. Si deseamos saber el área de nuestro terreno solo debemos contar las unidades exactas que caben dentro de el


Después de contar nos damos cuenta que hay exactamente 36 unidades cuadradas, pero este proceso de contar uno a uno nos toma más tiempo, es aquí donde podemos usar la multiplicación cómo un método de conteo más rápido y efectivo, así el procedimiento sería multiplicar 6u x 6u = 36u² (unidades cuadradas).
De manera igual calcule el área de los siguientes terrenos:
A partir de lo anterior podemos decir que:
Tal vez parezca algo inútil pero no es así. Imagina que desean decorar un poco tu hogar poniéndole baldosa al suelo, a la hora de comprar los materiales hay dos formas de saber cuanto llevaremos, una forma es simplemente dejarse llevar por el parecer y el resultado de esto sería comprar mas o menos material, la otra forma es calcular el área del terreno y dividirlo por el área de una baldosa, de esta ultima manera de seguro tendríamos un resultado mucho mas preciso.
Calculemos el resultado de los siguientes figuras, tomemos en cuenta que se aplica la misma formula para los rectangulos.
Como vemos el área no solo se limita a una sola unidad, ¿Crees que se puede saber cual es la equivalencia de una medida en otra unidad de medida distinta a la suya? Por ejemplo si tenemos un terreno 50000 m² ¿cuánto equivale esto en hectáreas? Miremos:
La hectárea (ha) el prefijo hecto significa «cien» y es una medida de superficie equivalente a 10000 m² (metros cuadrados).
Sabiendo esto para saber cuanto son 50000 m² en hectáreas lo que debemos hacer es el siguiente procedimiento:
una hectárea son 10000 m²
ahora:
Ahora para practicar convierta a m²:
10.5 ha 6.2 ha 8.6 ha
Pero también podemos convertir m² a otras unidades, por ejemplo a plazas. Miremos:
1 Plaza = 6400 m²
convirtamos 60000 m² a plazas
Supongamos que se tienen 5 terrenos A, B, C, D y E cuyas áreas son 6.3 plazas, 5 ha, 25000 m², 3000 m² y 600 km² respectivamente. A partir de esto calcule el área de las diferentes combinaciones de terrenos que aparecen en la siguiente tabla y exprese su resultado en la unidad de medida que se indica.
| A + D | E + B + A | C - D | E + C | B + D | C + A + D + B | |
| Resultado de la combinación | ||||||
| Unidad de medida | km² | m² | ha | Plazas | ha | km² |
Escala:
Miremos un sencillo ejemplo de que es y que representa una escala: Si observamos el siguiente dibujo podemos decir que su tamaño es de 1 unidad , pero en comparación con el objeto real este estará reducido 10 unidades.

La relación se representa así 1:10 lo que indica que para conocer el tamaño real del objeto debemos multiplicarlo por 10.
Entonces, si el largo del machete en el dibujo mide 10 cm la medida del machete real sera 100 cm. Así que podríamos decir que una escala es la relación que existe entre las medidas o dimensiones reales de un objeto y las de un dibujo que representa la realidad. Podríamos tomar por Escala como reducir o aumentar el tamaño de un objeto sin que este pierda sus proporciones o la relación que existe entre sus lados en el resultado final.
Por ejemplo: Supongamos que tenemos una casa en tamaño real (Figura A) y la deseamos escalar de manera que el dibujo ocupe el tamaño de una hoja de cuaderno, el resultado final seria el dibujo a su lado (Figura B).
| Real | Escala |
Como podemos apreciar hemos reducido el tamaño de la casa sin que esta pierda su proporción, podremos decir entonces que hemos escalado la casa.
Con este ejemplo podemos dar una idea intuitiva de lo que es una Escala, pero para ser mas exactos podemos pensar en los planos de una casa o edificio y también en las distancias que aparecen en los mapas, si alguna vez hemos visto un mapa este nos dirá la escala a la cual esta dada la relación con el territorio en la realidad.
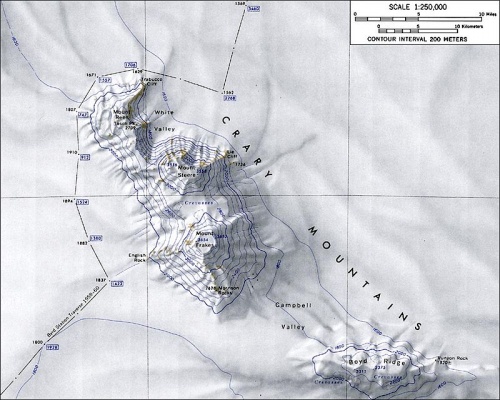
Mapa con escala de reducción 1:250.000 lo que significa que cada centímetro del mapa son 2.5 Kilómetros en la realidad.
En el ejemplo anterior nos dan dos medidas, una en centímetros y la otra Kilómetros, lo cual quiere decir que debemos saber como cambiar de unidades de medida.
Continuando con el estudio de las áreas, miremos que pasa si cortamos un cuadrado o un rectángulo por toda su diagonal.
Lo que obtendríamos sería dos triángulos rectángulos. Un triangulo rectángulo es aquel que cuenta con un ángulo recto ( que mide 90°) sus otros dos ángulos siempre son agudos ( que miden menos de 90°), ya que sabemos que un triangulo es la mitad de un rectángulo podremos decir que su formula es:
Base x altura pero ya que solo es la mitad de un rectángulo dividiremos esto en 2, así el área del triangulo es:
Calcule el área de los siguientes triángulos:

examinemos el circulo.
Partamos de un cuadrado, como ya sabemos cuenta con cuatro lados ¿ qué pasará si empezamos a incrementar sus lados indeterminadamente? Observemos:
Círculo
Así es como nace el circulo, ahora miremos sus partes.

El Radio: es el segmento que une el centro con un punto de la circunferencia, y por extensión también se dice de la longitud de éste.
El diámetro: es el segmento que une dos puntos de la circunferencia pasando por el centro. El diámetro divide al círculo en dos partes iguales.
Circunferencia: línea curva cerrada cuyos puntos equidistan de otro situado en el mismo plano que se llama centro.
Ya sabiendo esto supongamos que tenemos tres objetos circulares, un plato, una tapa de gaseosa y un vaso, necesitamos saber cual es la longitud de su circunferencia, lo que primero se nos puede atravesar por la cabeza es medirlos , llenemos la siguiente tabla:
| |
| ||
Pero este procedimiento de medir es bastante tedioso además de largo, intentemos una nueva forma y a partir de los resultado comparemos.
| |
| ||
| |
Como podemos apreciar cuando multiplicamos el diámetro de cada objeto por 3.14 nos da un resultado muy aproximado a la longitud de circunferencia que obtuvimos midiendo en la tabla anterior, esto demuestra que hay una forma mas rápida de obtener la longitud de circunferencia de un circulo, que el resultado no de exactamente no significa que este mal el procedimiento, esto pasa ya que no contamos con instrumentos de medida que nos den una certeza total de las medidas, por lo tanto podemos decir que:
Longitud de la circunferencia : 3.14 x Diámetro del circulo.
¿Sabes de a donde proviene el numero 3.14?, A este número se le conoce como pi y es representado por el símbolo π. El número Pi es el valor del cociente de la división de la longitud de una circunferencia entre su diámetro. Su valor aproximado es 3,14 pero en realidad π tiene infinitos decimales algunos de ellos son:
En la antigüedad, para el descubrimiento de este número las personas de aquella época hacían un circulo en la arena median su longitud de circunferencia y la dividían por su diámetro, con el paso de los tiempos esta teoría se fue fortaleciendo y hoy por hoy podemos decir que en todo circulo la longitud de su circunferencia dividido por su diámetro siempre dará pi.
Con todo lo anterior claro ahora si averigüemos como calcular el área de un circulo
Como nos muestra la imagen el área del circulo es
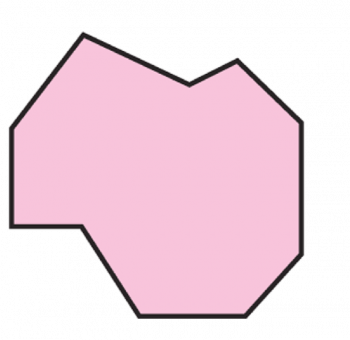
Ahora si queremos aplicar estas ideas del mundo abstracto al nuestro, encontraremos figuras que no tienen una formula para saber cual es su área, en ese caso podremos separar esa figura de forma extraña a unas figuras mas pequeñas que ya conocemos y con las cuales hemos trabajado con nuestro tutor o compañeros.
Digamos que tenemos un espacio para hacer piscicultura y tiene la siguiente forma:
para saber cual es el área del estanque debemos separar o descomponerlo en figuras que conozcamos, en este caso podemos ver que nuestro terreno tiene la forma de un Rectángulo y la mitad de un círculo (semi-círculo).
Como ya hemos trabajado con estas figuras antes sabemos que el área de un Rectángulo es bxh y la de un círculo es Pi(r) ² y como es medio círculo lo dividimos en 2, luego el área total es la suma de las áreas que encontramos de forma separada.
En la figura nos indican que la base del Rectángulo mide 19 y la altura 12, ahora si hacemos la separación podemos calcular las áreas por separado y luego sumarlas para hallar el área total:
Sabemos también que la altura del Rectángulo es el diámetro del semi-círculo y que el Radio es la mitad del diámetro:
Altura = Diametro ; (solo para este caso)
Radio = Diametro/2
Radio = 12/2 = 6
Área del semicirculo: Pi(r)² = Pi(6)² ; (recordemos que Pi = 3.14)
Entonces el área total es: área Rectángulo + área semi-círculo:
Ahora analicemos la siguiente figura:
por ejemplo, para esta figura podemos separarla en un semi-círculo, un triangulo y un rectángulo.
Ahora inténtalo con esta:
Recuerda, siempre que tengas que hallar el área de un terreno complicado debes descomponerlo en figuras comunes.
Volúmenes
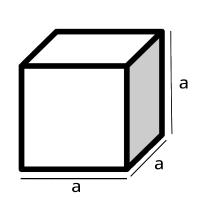
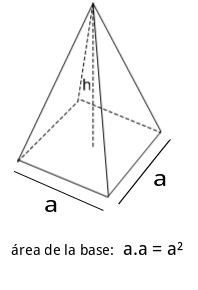
El volumen de un objeto es el espacio que ocupa, también podemos decir que es la capacidad de almacenamiento que tiene. Por ejemplo el volumen de una cubeta es la cantidad de agua que puede almacenar y para medir el volumen usamos unidades elevadas a la 3 (m³, cm³, dm³ , entre otras). En esta unida conoceremos el volumen de algunos prismas ¿Te suena familiar este concepto?, si nunca lo has escuchado pues averigüemos el significado de prisma. En geometría, un prisma es un poliedro (cuerpo geométrico cuyas caras son planas y encierran un volumen finito.) el cual tiene dos caras paralelas e iguales llamadas bases y sus caras laterales son paralelogramos. Por ejemplo:
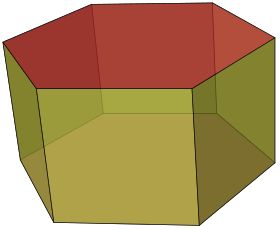
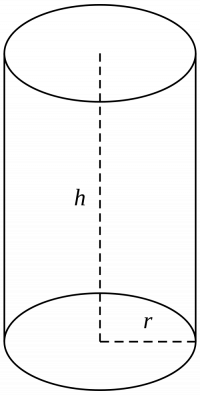
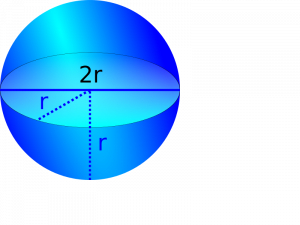
Como vimos antes hay áreas que tienen formas muy complejas para ser medidas, de manera similar hay cuerpos que debemos descomponer en otros cuerpos mas pequeños y conocidos para calcular su volumen. Hagamos un repaso de las figuras comunes:
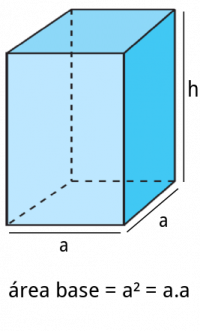
si echamos un vistazo sobre las formulas podemos ver que para todos los cuerpos (menos la esfera), se puede hallar el volumen multiplicando el área de la base y la altura del cuerpo.
Esta información es muy útil porque el prisma es un caso especial, el prisma puede tener una base en forma de triangulo, cuadrado (como la imagen en este documento), etc.
Por eso para hallar el volumen de un prisma encontramos el área de la base y la multiplicamos por su altura.
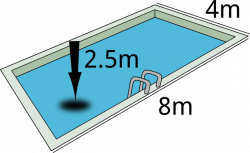
Calculemos el volumen de un prisma muy conocido, necesitamos saber el volumen de una piscina de 4m de ancho por 8m de largo y 2.5m de profundidad, tal como muestra la siguiente imagen:
Si nos fijamos bien una piscina es un prima.
Si deseamos calcular el volumen de esta figura lo que debemos hacer será multiplicar la altura por el ancho por el largo, si hacemos esto sabremos que el volumen de nuestra piscina es:
- Calcule el volumen de una mesa que mide 1.5m de ancho, 2m de largo y 5cm de espesor.
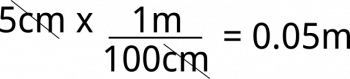
Como ya sabemos el volumen de un paralelepípedo es Área de la base x la altura así que multiplicamos 1.5m x 2m = 3m², ahora multiplicamos esto por la altura o el espesor que es 5cm, 3m² x 5cm ¿es posible realizar esta operación?, de echo esto no es posible primero debemos convertir bien sea m a cm o cm a m, Puesto que si convertimos m a cm obtendríamos un número algo grande es mas factible convertir cm a m así que realizamos el procedimiento que ya conocemos.
1m son 100cm ¿cuántos m son 5cm?
Ya sabiendo esto ahora si podremos multiplicar 3m² x 0,05m = 1,5 m³
Descomposición
Si quisiéramos calcular el volumen de un lápiz únicamente con las anteriores figuras, podríamos hacerlo?

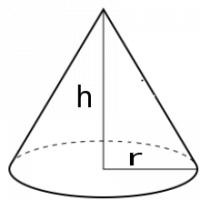
Por supuesto que sí, porque un lápiz como el de la imagen esta construido con un cono (en la punta), un cilindro (la parte de color amarillo) y media esfera (el borrador), así que tenemos que hallar el volumen del cono, del cilindro y la media esfera, para luego sumarla y el resultado es el volumen de todo el lápiz.
Hagamos el ejercicio juntos, toma un lápiz u objeto similar y procedamos:
vamos a separar el lápiz en tres partes, si quieres puedes usar la imaginación o partir un lápiz.
Primero separamos la punta que representa un cono, luego el cilindro y la media esfera que es el borrador.

ahora para hallar el volumen del cono (la punta) medimos su altura h y el radio r y aplicamos la formula.
Para el cilindro necesitamos también un radio r su altura h, pero el radio del cilindro y del cono es el mismo por lo tanto no tenemos que volver a medir el radio.
Para la media esfera solo necesitamos el radio, pero el radio es el mismo que el de los demás cuerpos así que no tenemos que volver a medir.
Ya para terminar sumamos el volumen de las tres figuras y el resultado es el volumen total.
Sencillo!!!
De manera igual se hace con todos los cuerpos.
Vídeo sugeridos
https://www.youtube.com/watch?v=wNVyN30MjZQ
Vídeos sugeridos
https://www.youtube.com/watch?v=JfSHpD9mWCc
https://www.youtube.com/watch?v=wRdvxPOnyM4