Diferencia entre revisiones de «Figuras tridimensionales»
(→Figuras Tridimensionales) |
(→Figuras Tridimensionales) |
||
| (No se muestran 65 ediciones intermedias del mismo usuario) | |||
| Línea 1: | Línea 1: | ||
| − | + | =Figuras Tridimensionales= | |
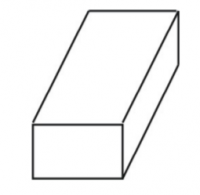
| − | Según el módulo de propiedades las figuras que | + | Según el módulo de propiedades las figuras que tú dibujas en una hoja de papel son bidimensionales puesto que solo se construyen con dos medidas, por ejemplo, ancho y largo. Mientras que en un objeto tridimensional aparece otra medida, la profundidad. Es decir, una figura tridimensional esta construida Por tres medidas, ancho, alto y profundidad como vemos en la siguiente figura (h:altura , a: ancho y p:profundidad). |
| − | [[Archivo: | + | <center>[[Archivo:G4081.png|200px|caption|center]]</center> |
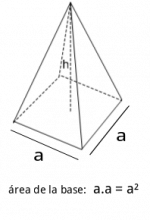
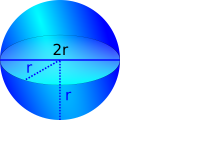
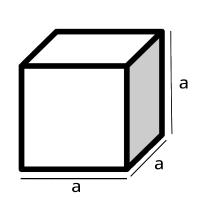
| + | Aunque una superficie plana tiene dos dimensiones, a partir de ellas podemos construir objetos tridimensionales. A continuación se representan en forma bidimensional y tridimensional las figuras geométricas más conocidas por todos nosotros. | ||
| − | |||
| − | |||
| + | <center> | ||
| + | {| border=1 cellspacing=0 cellpadding=5 | ||
| + | |Bidimensional | ||
| + | |Tridimensional | ||
| + | |- | ||
| + | |[[Archivo:triangulo.png|150px|caption|center]] | ||
| + | ||[[Archivo:piramide.png|150px|caption|center]] | ||
| + | |- | ||
| + | ||[[Archivo:circle.png|150px|caption|center]] | ||
| + | |[[Archivo:esfera.png|200px|caption|center]] | ||
| + | |- | ||
| + | |[[Archivo:cuadrilatero.png|150px|caption|center]] | ||
| + | |[[Archivo:cubo.png|200px|caption|center]] | ||
| + | |} | ||
| + | </center> | ||
| − | |||
| − | |||
| + | <h3>Introducción:</h3> | ||
| − | + | La mejor forma de representar una figura tridimensional es usar un modelo del sólido. Desafortunadamente, los modelos algunas veces no están disponibles. Existen cuatro formas primarias de representar sólidos en dos dimensiones sobre el papel. Estas son: | |
| − | + | -Una vista isométrica(o perspectiva). | |
| + | -Una vista ortográfica o al vuelo . | ||
| − | + | -Una vista en sección transversal. | |
| − | + | -Una red (malla). | |
| − | + | <h3>Vista isométrica:</h3> | |
| − | + | La típica forma de ver un objeto tridimensional es la vista isométrica . Estrictamente hablando, la vista isométrica de un sólido no incluye perspectiva. Entiendase por perspectiva como la ilusión usada para dar una idea de la posición, el volumen y situación en que se encuentra un objeto. | |
| − | + | La vista isométrica es la manera de gráficar un objeto tridimensional en dos dimensiones, en otras palabras seria dibujar un objeto tridimendisional sobre un papel, el tablero o inclusive el suelo. | |
| − | La | + | |
| − | + | <center> | |
| − | + | {| border=1 cellspacing=0 cellpadding=5 | |
| − | + | |[[Archivo:32.png|150px|caption|center]] | |
| − | + | |[[Archivo:34.png|150px|caption|center]] | |
| + | |[[Archivo:35.png|150px|caption|center]] | ||
| + | |} | ||
| + | </center> | ||
| + | Las figuras de abajo muestran la diferencia entre una vista isométrica y una vista en perspectiva de un sólido. | ||
| − | + | <center>[[Archivo:36.png|400px|caption|center]]</center> | |
| − | + | Como puedes ver, la vista en perspectiva luce más “real” al ojo, pero en geometría, las representaciones isométricas son útiles para medir y comparar distancias. | |
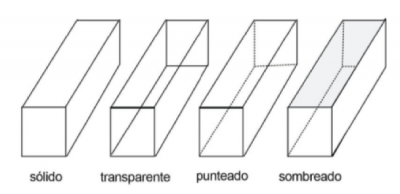
| − | + | A la vista isométrica con frecuencia se le muestra en una forma transparente o forma “ver a través”. | |
| − | [[Archivo: | + | <center>[[Archivo:38.png|400px|caption|center]]</center> |
| − | + | ||
| − | + | Color y sombras también pueden ser agregadas para ayudar al ojo a visualizar el sólido. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Ejemplo 1 | Ejemplo 1 | ||
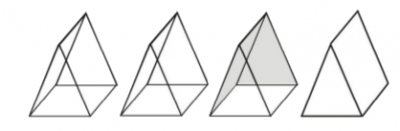
| − | Mostrar vistas | + | Mostrar las vistas isométricas de un prisma con una base triangular. |
| − | [[Archivo:39.png|400px|caption|center]] | + | <center>[[Archivo:39.png|400px|caption|center]]</center> |
Ejemplo 2 | Ejemplo 2 | ||
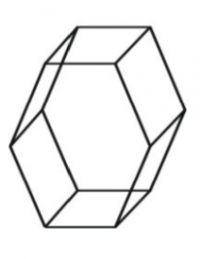
| − | Mostrar | + | Mostrar la vista isométrica en forma transparente de un prisma con una base hexagonal. |
| − | [[Archivo:40.png|200px|caption|center]] | + | <center>[[Archivo:40.png|200px|caption|center]]</center> |
| − | Vista ortográfica | + | <h3>Vista ortográfica</h3> |
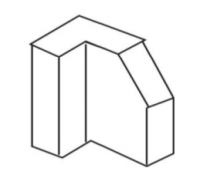
| − | Una proyección ortográfica es una vista | + | Una proyección ortográfica es una vista de 90 ° de un sólido, la cual muestra una representación clara de cada uno de los lados de la figura dada. Una buena forma de ver cómo trabaja una proyección ortográfica es construir una. Por ejemplo, el poliedro (una figura con muchas caras) no convencional mostrado continuación, tiene una proyección ortográfica en cada lado diferente en cada lado. |
| − | [[Archivo: | + | <center> |
| + | {| border=1 cellspacing=0 cellpadding=5 | ||
| + | | [[Archivo:1111.png|200px|caption|center]] | ||
| + | | [[Archivo:43.png|200px|caption|center]] | ||
| + | |} | ||
| + | </center> | ||
| − | + | <h3>Mallas</h3> | |
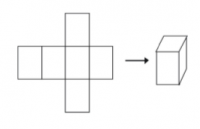
| − | + | Una última forma de representar un sólido es usar una red. Si tú cortas una red, puedes doblarla en un modelo de una figura. Las redes pueden usarse también para analizar un sólido. Aquí hay un ejemplo de una red para un cubo. | |
| − | + | <center>[[Archivo:53.png|200px|caption|center]] | |
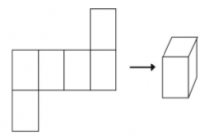
| − | + | Existe más de una manera para hacer una red para una figura individual. | |
| − | + | [[Archivo:54.png|200px|caption|center]] | |
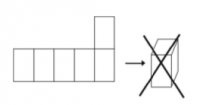
| − | + | De cualquier forma, no todos los arreglos crearán un cubo. | |
| − | + | [[Archivo:55.png|200px|caption|center]] | |
| − | + | Ejemplo 7: Qué clase de figura crea la red? Dibujar la figura. | |
| − | + | [[Archivo:56.png|200px|caption|center]] | |
| − | |||
| − | + | La red crea un prisma rectangular en forma de caja como se muestra abajo. | |
| − | |||
| − | + | [[Archivo:57.png|200px|caption|center]] | |
| − | + | </center> | |
| − | [[Archivo: | + | Ejemplo 3 |
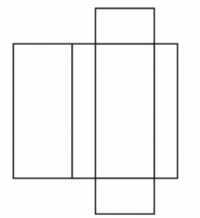
| + | Qué clase de red puedes dibujar para representar la figura mostrada? Dibujar la red. | ||
| + | <center> | ||
| + | [[Archivo:58.png|200px|caption|center]] | ||
| − | + | Es mostrada una red para el prisma . Otras redes son posibles. | |
| − | [[Archivo: | + | [[Archivo:59.png|200px|caption|center]] |
| − | + | </center> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Revisión actual del 17:47 12 dic 2016
Contenido
Figuras Tridimensionales
Según el módulo de propiedades las figuras que tú dibujas en una hoja de papel son bidimensionales puesto que solo se construyen con dos medidas, por ejemplo, ancho y largo. Mientras que en un objeto tridimensional aparece otra medida, la profundidad. Es decir, una figura tridimensional esta construida Por tres medidas, ancho, alto y profundidad como vemos en la siguiente figura (h:altura , a: ancho y p:profundidad).
Aunque una superficie plana tiene dos dimensiones, a partir de ellas podemos construir objetos tridimensionales. A continuación se representan en forma bidimensional y tridimensional las figuras geométricas más conocidas por todos nosotros.
| Bidimensional | Tridimensional |
Introducción:
La mejor forma de representar una figura tridimensional es usar un modelo del sólido. Desafortunadamente, los modelos algunas veces no están disponibles. Existen cuatro formas primarias de representar sólidos en dos dimensiones sobre el papel. Estas son:
-Una vista isométrica(o perspectiva).
-Una vista ortográfica o al vuelo .
-Una vista en sección transversal.
-Una red (malla).
Vista isométrica:
La típica forma de ver un objeto tridimensional es la vista isométrica . Estrictamente hablando, la vista isométrica de un sólido no incluye perspectiva. Entiendase por perspectiva como la ilusión usada para dar una idea de la posición, el volumen y situación en que se encuentra un objeto.
La vista isométrica es la manera de gráficar un objeto tridimensional en dos dimensiones, en otras palabras seria dibujar un objeto tridimendisional sobre un papel, el tablero o inclusive el suelo.
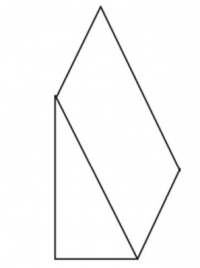
Las figuras de abajo muestran la diferencia entre una vista isométrica y una vista en perspectiva de un sólido.
Como puedes ver, la vista en perspectiva luce más “real” al ojo, pero en geometría, las representaciones isométricas son útiles para medir y comparar distancias.
A la vista isométrica con frecuencia se le muestra en una forma transparente o forma “ver a través”.
Color y sombras también pueden ser agregadas para ayudar al ojo a visualizar el sólido.
Ejemplo 1 Mostrar las vistas isométricas de un prisma con una base triangular.
Ejemplo 2 Mostrar la vista isométrica en forma transparente de un prisma con una base hexagonal.
Vista ortográfica
Una proyección ortográfica es una vista de 90 ° de un sólido, la cual muestra una representación clara de cada uno de los lados de la figura dada. Una buena forma de ver cómo trabaja una proyección ortográfica es construir una. Por ejemplo, el poliedro (una figura con muchas caras) no convencional mostrado continuación, tiene una proyección ortográfica en cada lado diferente en cada lado.
Mallas
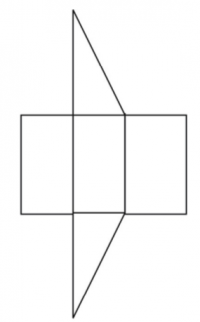
Una última forma de representar un sólido es usar una red. Si tú cortas una red, puedes doblarla en un modelo de una figura. Las redes pueden usarse también para analizar un sólido. Aquí hay un ejemplo de una red para un cubo.
Existe más de una manera para hacer una red para una figura individual.
De cualquier forma, no todos los arreglos crearán un cubo.
Ejemplo 7: Qué clase de figura crea la red? Dibujar la figura.
La red crea un prisma rectangular en forma de caja como se muestra abajo.
Ejemplo 3 Qué clase de red puedes dibujar para representar la figura mostrada? Dibujar la red.
Es mostrada una red para el prisma . Otras redes son posibles.