Diferencia entre revisiones de «Proporciones directas e inversas»
| Línea 9: | Línea 9: | ||
| − | PROPORCIONALIDAD DIRECTA | + | =PROPORCIONALIDAD DIRECTA= |
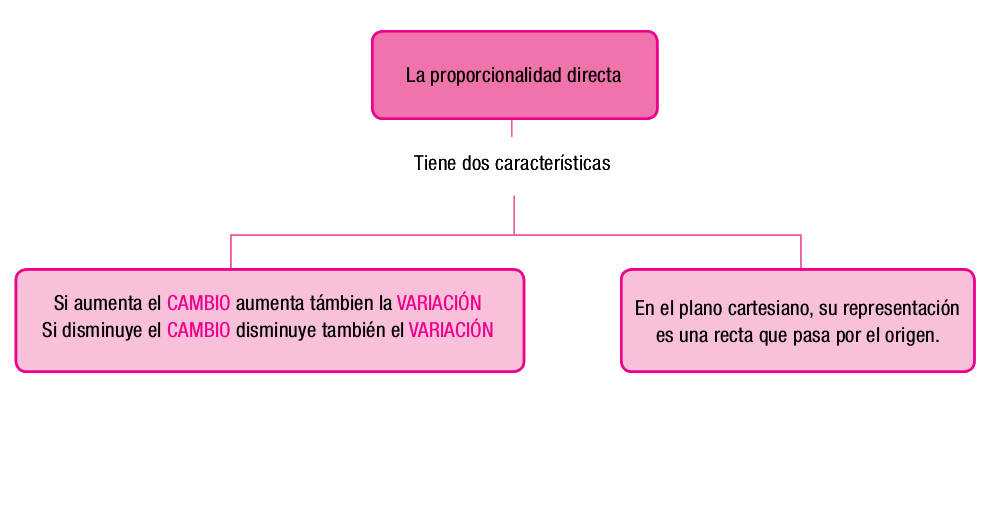
Concepto. Dos magnitudes son directamente proporcionales si al aumentar una, aumenta también la otra; si al disminuir la primera, la segunda también disminuye y, además, tiene cociente constante. En este caso se dice que existe proporcionalidad directa y la representación gráfica es una línea recta que pasar por el origen del plano cartesiano. También, Si se tiene 2 cantidades tales que al mutiplicar una de ellas por un número la otra queda multiplicada por el mismo número, o al dividir una de ellas la otra queda dividida por el mismo número, se dice que las cantidades son directamente proporcionales | Concepto. Dos magnitudes son directamente proporcionales si al aumentar una, aumenta también la otra; si al disminuir la primera, la segunda también disminuye y, además, tiene cociente constante. En este caso se dice que existe proporcionalidad directa y la representación gráfica es una línea recta que pasar por el origen del plano cartesiano. También, Si se tiene 2 cantidades tales que al mutiplicar una de ellas por un número la otra queda multiplicada por el mismo número, o al dividir una de ellas la otra queda dividida por el mismo número, se dice que las cantidades son directamente proporcionales | ||
| + | |||
| + | [[Archivo:21.png|1000px|caption|center]] | ||
| + | |||
| + | Ejemplo: Si 18 lapices cuestan $28, entonces 54 lápices constarán el triple, es decir, $ 84; al multiplicar el número de lápices por 3 el costo también quedó multiplicado por 3, por lo tanto, las cantidades son directamente proporcionales. | ||
| + | |||
| + | Ejemplo: La ilustración muestra una secuencia de cuadrados, que va aumentando de acuerdo al tamaño del lado. Así: EL primer cuadrado tiene 1 cm de lado, es segundo tiene 2 m, el tercero tiene 3 cm y el cuarto cuadro tiene 4 cm. | ||
[[Archivo:21.png|1000px|caption|center]] | [[Archivo:21.png|1000px|caption|center]] | ||
Revisión del 18:34 11 nov 2016
Introducción proporciones directas e inversas
Hoy en día vemos las proporciones en los diseños arquitectónicos, en la solución de diferentes problemas de ingeniería y en la vida cotidiana en el sector rural y entre muchos otros campos. Para entender mejor el concepto de proporciones hay que tener en cuenta el concepto de razón y ver su utilidad en la solución práctica de problemas que tiene ver con situaciones cotidianas, como por Ejemplo en las construcciones rurales…
En este capítulo encontraremos una serie de conceptos: Proporcionalidad directa e inversa, Razón, proporción y ejemplos que amplían estas definiciones; que nos ayudan a crear la destreza de interpretar, graficar y solucionar situaciones de la vida rural, y a la vez para darle cumplimiento a los estándares básicos de competencias en matemáticas.
PROPORCIONALIDAD DIRECTA
Concepto. Dos magnitudes son directamente proporcionales si al aumentar una, aumenta también la otra; si al disminuir la primera, la segunda también disminuye y, además, tiene cociente constante. En este caso se dice que existe proporcionalidad directa y la representación gráfica es una línea recta que pasar por el origen del plano cartesiano. También, Si se tiene 2 cantidades tales que al mutiplicar una de ellas por un número la otra queda multiplicada por el mismo número, o al dividir una de ellas la otra queda dividida por el mismo número, se dice que las cantidades son directamente proporcionales
Ejemplo: Si 18 lapices cuestan $28, entonces 54 lápices constarán el triple, es decir, $ 84; al multiplicar el número de lápices por 3 el costo también quedó multiplicado por 3, por lo tanto, las cantidades son directamente proporcionales.
Ejemplo: La ilustración muestra una secuencia de cuadrados, que va aumentando de acuerdo al tamaño del lado. Así: EL primer cuadrado tiene 1 cm de lado, es segundo tiene 2 m, el tercero tiene 3 cm y el cuarto cuadro tiene 4 cm.